摘要:解析及点评: 1解析:设出单位向量的坐标.通过解方程组解得答案为(C). 点评:注意选项的区别. 2解析:根据函数本身的限制.列出不等式组.解得结果为(D). 点评:被开方数应为非负数.对数的真数要为正数. 3解析: 因为A类学校占三类学校人数的.故抽取A类试卷份数为.选(B). 点评:本题是对新增内容的考查.要求对基本知识要熟练掌握. 4解析:m∥n 能推得D.但D不能推得m∥n.故答案为(D). 点评:了解线面位置关系的特征. 5解析:令a+b=t.则.易得答案(B). 点评:本题解题过程中用到了换元法. 6解析:由得离心率是.选(B). 点评:由条件构造出关于离心率e的方程解题. 7解析:f(x)既是偶函数.又是周期函数.利用图象可得交点个数为6.选(C). 点评:本题是对函数综合性质的考查. 8解析:将转化为动点P到定点A的距离与到准线距离之和来考虑.最小值为.选(C). 点评:将数与形有机结合.可寻求到解题捷径. 9解析:利用原函数和反函数图象的对称性.得= -2.选(D). 点评:原函数和反函数图象关于直线y=x对称. 10解析:c的范围满足.其一个值是3.选(C). 点评:利用圆心到直线距离.可得心应手地解题. 11解析:由条件.关于x的不等式ax-b>0的解集是.得a>0.且a=b.代入分式不等式解得.选(A). 点评:函数.方程与不等式之间有着天然的联系. 12解析:个位数字与百位数字之差的绝对值等于8.有0.8与1.9两类.符合条件的四位数有210个.选(C). 点评:解排列组合问题.应“先分类.再分步 . 13解析:用等积法求得点到面的距离是 . 点评:求点到平面距离.可直接作垂线段.用等积法也是行之有效的. 14解析:..用裂项法求得和为 . 点评:需要掌握等差与等比两个基本数列求和公式.同时也要掌握“裂项法 等求和法. 15解析:所以sin.= . 点评:倍角关系是相对的.要认识其中的辩证关系. 16解析:经过t秒钟后.P.Q的坐标分别为P.Q.根据条件.利用它们的数量积为0.解得t=2 . 点评:本题如果从物理的角度来理解会更流畅.反映了多学科的交汇作用.
网址:http://m.1010jiajiao.com/timu3_id_498927[举报]
已知函数f(x)=
(a>0且a≠1),设函数g(x)=f(x-
)+1.
(1)求证:f(x)是奇函数;
(2)求g(x)+g(1-x)及g( 0 )+g(
)+g(
)+g(
)+g( 1 )的值;
(3)是否存在正整数a,使不等式
>n2对一切n∈N*都成立,若存在,求出正整数a的最小值;不存在,说明理由;
(4)结合本题加以推广:设F(x)是R上的奇函数,请你写出一个函数G(x)的解析式;并根据第(2)小题的结论,猜测函数G(x)满足的一般性结论.
查看习题详情和答案>>
| ax-1 |
| ax+1 |
| 1 |
| 2 |
(1)求证:f(x)是奇函数;
(2)求g(x)+g(1-x)及g( 0 )+g(
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
(3)是否存在正整数a,使不等式
| ||
| g(1-n) |
(4)结合本题加以推广:设F(x)是R上的奇函数,请你写出一个函数G(x)的解析式;并根据第(2)小题的结论,猜测函数G(x)满足的一般性结论.
已知△ABC中,AC=1,∠ABC=
,∠BAC=x,记f(x)=
•
.
(1)求f(x)解析式及定义域;
(2)设g(x)=6m•f(x)+1,x∈(0,
),是否存在正实数m,使函数g(x)的值域为(1,
]?若存在,请求出m的值;若不存在,请说明理由.
查看习题详情和答案>>
| 2π |
| 3 |
| AB |
| BC |
(1)求f(x)解析式及定义域;
(2)设g(x)=6m•f(x)+1,x∈(0,
| π |
| 3 |
| 3 |
| 2 |
设f(x)=
且a≠1),函数y=g(x)的图象与函数y=f(x)图象关于直线x-y=0对称.
(1)求函数y=g(x)的解析式及定义域;
(2)设关于x的方程loga
=g(x)在[2,6]上有实数解,求t的取值范围;
(3)当a=e(e为自然对数的底数)时,证明:
g(k)>
.
查看习题详情和答案>>
| 1+ax |
| 1-ax |
(1)求函数y=g(x)的解析式及定义域;
(2)设关于x的方程loga
| t |
| (x2-1)(7-x) |
(3)当a=e(e为自然对数的底数)时,证明:
| n |
 |
| k=2 |
| 2-n-n2 | ||
|
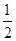 .
.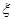 ,求
,求 ,其中
,其中 .
. 时,设
时,设 ,
, ,求
,求 的解析式及定义域;
的解析式及定义域; 时,求
时,求 的最小值;
的最小值; ,当
,当 时,
时, 对任意
对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围.