如图，在三棱锥P-ABC中，AB⊥BC，AB=BC=kPA，点O、D分别是AC、PC的中点，OP⊥底面ABC．
（Ⅰ）求证：OD∥平面PAB；
（Ⅱ）当k=

1

2

时，求直线PA与平面PBC所成角的正弦值；
（Ⅲ）当k取何值时，O在平面PBC内的射影恰好为△PBC的重心？
（注：若△ABC的三点坐标分别为A（x₁，y₁，z₁），B（x₂，y₂，z₂），C（x₃，y₃，z₃），则该三角形的重心坐标为：(

x1+x2+x3

3

，

y1+y2+y3

3

，

z1+z2+z3

3

)．）

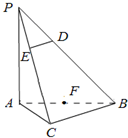如图，在三棱锥P-ABC中，底面ABC为等腰直角三角形，∠ACB=90°，棱PA垂直底面ABC，PA=AB=4，BD=

3

4

BP，CE=

3

4

BC，F是AB的中点．
（1）证明DE∥平面ABC；
（2）证明：BC⊥平面PAC；
（3）求四棱锥C-AFDP的体积．

如图，在三棱锥P-ABC中，AC=BC=2，∠ACB=90°，AP=BP，PC⊥AC．
（Ⅰ）求证：PC⊥AB；
（Ⅱ）设二面角P-AB-C的大小为θ，θ∈[

π

6

，

π

2

)，求二面角B-AP-C的余弦值的范围．

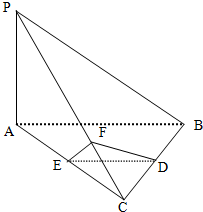如图，在三棱锥P-ABC中，PA=3，AC=AB=4，PB=PC=BC=5，D、E分别是BC、AC的中点，F为PC上的一点，且PF：FC=3：1．
（Ⅰ）求证：PA⊥BC；
（Ⅱ）试在PC上确定一点G，使平面ABG∥平面DEF；
（Ⅲ）求三棱锥P-ABC的体积．