摘要：8．圆方程(x-1)2+(y+1)2=4.则圆心到直线x-y-4=的距离为( ) A. B. C.2 D.-
网址：http://m.1010jiajiao.com/timu3_id_498641[举报]
本题有（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
（1）选修4-2：矩阵与变换
已知矩阵
（Ⅰ）求矩阵NN；
（Ⅱ）若点P（0，1）在矩阵M对应的线性变换下得到点P′，求P′的坐标．
（2）选修4-4：坐标系与参数方程
在直角坐标系xOy中，直线l的参数方程是
（t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的极坐标方程是ρ=2cosθ（Ⅰ）在直角坐标系xOy中，求圆C的直角坐标方程
（Ⅱ）求圆心C到直线l的距离．
（3）选修4-5：不等式选讲
已知函数f（x）=|x-1|
（Ⅰ）解不等式f（x）＞2；
（Ⅱ）求函数y=f（-x）+f（x+5）的最小值．
查看习题详情和答案>>
（1）选修4-2：矩阵与变换
已知矩阵
（Ⅰ）求矩阵NN；
（Ⅱ）若点P（0，1）在矩阵M对应的线性变换下得到点P′，求P′的坐标．
（2）选修4-4：坐标系与参数方程
在直角坐标系xOy中，直线l的参数方程是
（t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的极坐标方程是ρ=2cosθ（Ⅰ）在直角坐标系xOy中，求圆C的直角坐标方程（Ⅱ）求圆心C到直线l的距离．
（3）选修4-5：不等式选讲
已知函数f（x）=|x-1|
（Ⅰ）解不等式f（x）＞2；
（Ⅱ）求函数y=f（-x）+f（x+5）的最小值．
查看习题详情和答案>>
已知圆C：（x-3）2+（y-4）2=4和直线l：x+2y+2=0，直线m经过圆C外定点A（1，0）．
（1）若m与圆C相交于P，Q两点，问：当圆心C到直线m距离取何值时，三角形CPQ的面积取最大值，并写出此时m的直线方程；
（2）若直线m与圆C相交于P，Q两点，与l交于N点，且线段PQ的中点为M，则判断|AM|•|AN|是否为定值，若是求出定值，若不是说明理由． 查看习题详情和答案>>
（1）若m与圆C相交于P，Q两点，问：当圆心C到直线m距离取何值时，三角形CPQ的面积取最大值，并写出此时m的直线方程；
（2）若直线m与圆C相交于P，Q两点，与l交于N点，且线段PQ的中点为M，则判断|AM|•|AN|是否为定值，若是求出定值，若不是说明理由． 查看习题详情和答案>>
已知圆C：（x-3）2+（y-4）2=4和直线l：x+2y+2=0，直线m经过圆C外定点A（1，0）．
（1）若m与圆C相交于P，Q两点，问：当圆心C到直线m距离取何值时，三角形CPQ的面积取最大值，并写出此时m的直线方程；
（2）若直线m与圆C相交于P，Q两点，与l交于N点，且线段PQ的中点为M，则判断|AM|•|AN|是否为定值，若是求出定值，若不是说明理由．
查看习题详情和答案>>
（1）若m与圆C相交于P，Q两点，问：当圆心C到直线m距离取何值时，三角形CPQ的面积取最大值，并写出此时m的直线方程；
（2）若直线m与圆C相交于P，Q两点，与l交于N点，且线段PQ的中点为M，则判断|AM|•|AN|是否为定值，若是求出定值，若不是说明理由．
查看习题详情和答案>>
下面给出的四个命题中：
①以抛物线y2=4x的焦点为圆心，且过坐标原点的圆的方程为（x-1）2+y2=1；
②若m=-2，则直线（m+2）x+my+1=0与直线（m-2）x+（m+2）y-3=0相互垂直；
③命题“?x∈R，使得x2+3x+4=0”的否定是“?x∈R，都有x2+3x+4≠0”；
④将函数y=sin2x的图象向右平移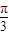
个单位，得到函数y=sin（2x-
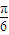）的图象．
其中是真命题的有 （将你认为正确的序号都填上）． 查看习题详情和答案>>
①以抛物线y2=4x的焦点为圆心，且过坐标原点的圆的方程为（x-1）2+y2=1；
②若m=-2，则直线（m+2）x+my+1=0与直线（m-2）x+（m+2）y-3=0相互垂直；
③命题“?x∈R，使得x2+3x+4=0”的否定是“?x∈R，都有x2+3x+4≠0”；
④将函数y=sin2x的图象向右平移
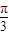个单位，得到函数y=sin（2x-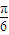）的图象．其中是真命题的有 （将你认为正确的序号都填上）． 查看习题详情和答案>>
| |||||
x∈R，使得x2＋3x＋4＝0”的否定是“
x∈R，都有x2＋3x＋4≠0”；
个单位，得到函数y＝sin(2x－
)的图象．