摘要:11.如图所示.双曲线的中心在坐标原点.焦点在x轴上.F1.F2分别为左.右焦点.双曲线的左支上有一点P.∠F1PF2=.且△PF1F2的面积为2.又双曲线的离心率为2.求该双曲线的方程. 解:设双曲线方程为:-=1(a>0.b>0). F1(-c,0).F2(c,0).P(x0.y0). 在△PF1F2中.由余弦定理.得: |F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|·cos=(|PF1|-|PF2|)2+|PF1|·|PF2|. 即4c2=4a2+|PF1|·|PF2|. 又∵S△PF1F2=2. ∴|PF1|·|PF2|·sin=2. ∴|PF1|·|PF2|=8. ∴4c2=4a2+8.即b2=2. 又∵e==2.∴a2=. ∴双曲线的方程为:-=1.
网址:http://m.1010jiajiao.com/timu3_id_497686[举报]
 如图所示,双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的左支上有一点P,∠F1PF2=
如图所示,双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的左支上有一点P,∠F1PF2=| π |
| 3 |
| 3 |
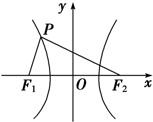 如图所示,双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的左支上有一点P,∠F1PF2=
如图所示,双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的左支上有一点P,∠F1PF2= ,且△PF1F2的面积为2
,且△PF1F2的面积为2 ,又双曲线的离心率为2,求该双曲线的方程.
,又双曲线的离心率为2,求该双曲线的方程.
查看习题详情和答案>>
如图所示,双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的左支上有一点P,∠F1PF2=
,且△PF1F2的面积为2
,又双曲线的离心率为2,求该双曲线的方程.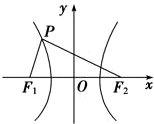
查看习题详情和答案>>
| π |
| 3 |
| 3 |

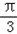 ,且△PF1F2的面积为2
,且△PF1F2的面积为2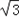 ,又双曲线的离心率为2,求该双曲线的方程.
,又双曲线的离心率为2,求该双曲线的方程.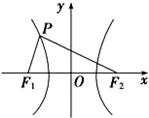
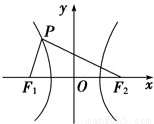 如图所示,双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的左支上有一点P,∠F1PF2=
如图所示,双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的左支上有一点P,∠F1PF2=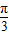 ,且△PF1F2的面积为2
,且△PF1F2的面积为2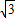 ,又双曲线的离心率为2,求该双曲线的方程.
,又双曲线的离心率为2,求该双曲线的方程.