摘要：如图,在三角形ABC中,若AC=3,BC=4,AB=5,以AB所在直线为轴,将此三角形旋转一周,求所得旋转体的表面积和体积. 解:如图所示,所得旋转体是两个底面重合的圆锥,高的和为AB=5.底面半径等于CO=,所以所得旋转体的表面积S=π·OC·=π··(3+4)=π;其体积V=·π·OC2·AO+·π·OC2·BO=·π·OC2·AB=π. 评析:求一些组合体的表面积和体积时,首先要弄清楚它由哪些基本几何体构成,再通过轴截面分析和解决问题.
网址：http://m.1010jiajiao.com/timu3_id_497661[举报]
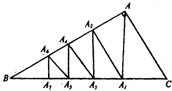如图，在Rt△ABC中，∠BAC=90°，作AA1⊥BC，A1A2⊥AB，A2A3⊥BC，A3A4⊥AB，A4A5⊥BC，A5A6⊥AB，A6A7⊥BC，A1，A2，A3，A4，A5，A6，A7分别为垂足：（1）△CAA1，△A1A2A3，△A3A4A5，△A5A6A7的周长和面积是否分别成等比数列？试给出证明．
（2）若AB=4，BC=5，分别求出（1）题中4个三角形的周长和△A1A2A3的面积．
（3）如果把题设中的作法一直进行下去，并把所得类同于（1）题中的4个三角形的所有三角形的面积从大到小排成一个数列{Sn}，设AB=c，AC=b，求{Sn}的通项公式和△A11A12A13的面积． 查看习题详情和答案>>
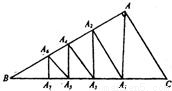
如图，在Rt△ABC中，∠BAC=90°，作AA1⊥BC，A1A2⊥AB，A2A3⊥BC，A3A4⊥AB，A4A5⊥BC，A5A6⊥AB，A6A7⊥BC，A1，A2，A3，A4，A5，A6，A7分别为垂足：
（1）△CAA1，△A1A2A3，△A3A4A5，△A5A6A7的周长和面积是否分别成等比数列？试给出证明．
（2）若AB=4，BC=5，分别求出（1）题中4个三角形的周长和△A1A2A3的面积．
（3）如果把题设中的作法一直进行下去，并把所得类同于（1）题中的4个三角形的所有三角形的面积从大到小排成一个数列{Sn}，设AB=c，AC=b，求{Sn}的通项公式和△A11A12A13的面积．
查看习题详情和答案>>
（1）△CAA1，△A1A2A3，△A3A4A5，△A5A6A7的周长和面积是否分别成等比数列？试给出证明．
（2）若AB=4，BC=5，分别求出（1）题中4个三角形的周长和△A1A2A3的面积．
（3）如果把题设中的作法一直进行下去，并把所得类同于（1）题中的4个三角形的所有三角形的面积从大到小排成一个数列{Sn}，设AB=c，AC=b，求{Sn}的通项公式和△A11A12A13的面积．
查看习题详情和答案>>