摘要：如图.在三棱柱ABC-A1B1C1中.侧棱AA1⊥底面ABC.底面是以∠ABC为直角的等腰直角三角形.AC＝2a.BB1＝3a.D是A1C1的中点.点F在线段AA1上.当AF＝ 时.CF⊥平面B1DF. 解析:由题意易知.B1D⊥平面ACC1A1.所以B1D⊥CF. 要使CF⊥平面B1DF. 只需CF⊥DF即可. 令CF⊥DF.设AF＝x. 则A1F＝3a-x. 由Rt△CAF∽Rt△FA1D.得＝. 即＝. 整理得x2-3ax+2a2＝0. 解得x＝a或x＝2a. 答案:a或2a
网址：http://m.1010jiajiao.com/timu3_id_497644[举报]
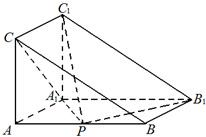如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AC⊥AB，AC=AA1=1，AB=2，P为线段AB上的动点．（I）求证：CA1⊥C1P；
（II）若四面体P-AB1C1的体积为
| 1 | 6 |
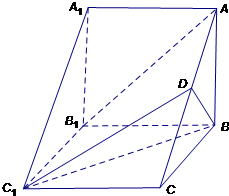如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，A1A=AB=2，BC=3．（1）求证：AB1∥平面BC1D；
（2）求四棱锥B-AA1C1D的体积． 查看习题详情和答案>>
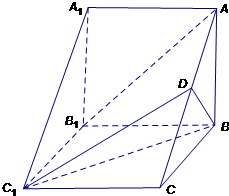如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，A1A=AB=2．（1）求证：AB1∥平面BC1D；
（2）若四棱锥B-AA1C1D的体积为3，求二面角C-BC1-D的正切值． 查看习题详情和答案>>
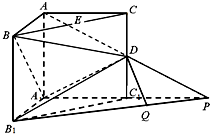如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面A1B1C1，∠BAC=90°，AB=AC=AA1=1，D是棱CC1的中点，P是AD的延长线与A1C1的延长线的交点．
如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB⊥AC，BC=1，AB=