摘要: (2011山东泰安.29 .10分)已知:在△ABC中.AC=BC.∠ACB=900.点D是AB的中点.点E是AB边上一点. (1)直线BF垂直于CE于点F.交CD于点G.求证:AE=CG, (2)直线AH垂直于CE于.垂足为H.交CD的延长线于点M.找出图中与BE相等的线段.并说明. [答案](1)证明:∵点D是AB中点.AC=BC.∠ACB=900 ∴CD⊥AB.∠ACD=∠BCD=450 ∠CAD=∠CBD=450 ∴∠CAE=∠BCG 又BF⊥CE ∴∠CBG+∠BCG=900 又∠ACE+∠BCF=900 ∴∠ACE=∠CBG ∴△AEC≌△CGB ∴AE=CG (2)BE=CM 证明:∵CH⊥HM.CD⊥ED ∴∠CMA+∠MCH=900 ∠BEC+∠MCH=900 ∴∠CMA=∠BEC 又.AC=BC.∠ACM=∠CBE=450 ∴△BCE≌△CAM ∴BE=CM
网址:http://m.1010jiajiao.com/timu3_id_496631[举报]
(1)已知,如图△ABC中,∠A=90°,∠B=67.5°.请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来,只需画图,不必说明理由,但要在图中标出相等两角的度数)

(2)已知:在△ABC中,∠C是其最小的内角,过点B的一条直线BD把这个三角形分割成两个等腰三角形,直线BD交AC边于点D.
①若∠C是△BCD的顶角,请探求∠ABC与∠C之间的关系;
②若∠C是△BCD的底角,∠BDC是△BCD的顶角.请探求∠ABC与∠C之间的关系;
③是否存在∠C是底角且∠CBD是顶角的等腰△BCD?若存在,请探求∠ABC与∠C之间的关系;若不存在,说明理由.
查看习题详情和答案>>

(2)已知:在△ABC中,∠C是其最小的内角,过点B的一条直线BD把这个三角形分割成两个等腰三角形,直线BD交AC边于点D.
①若∠C是△BCD的顶角,请探求∠ABC与∠C之间的关系;
②若∠C是△BCD的底角,∠BDC是△BCD的顶角.请探求∠ABC与∠C之间的关系;
③是否存在∠C是底角且∠CBD是顶角的等腰△BCD?若存在,请探求∠ABC与∠C之间的关系;若不存在,说明理由.
 已知:在△ABC中,AB=AC=2a,∠ABC=∠ACB=15° 求:S△ABC.
已知:在△ABC中,AB=AC=2a,∠ABC=∠ACB=15° 求:S△ABC.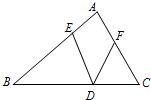 12、如图,已知:在△ABC中,∠A=80°,BD=BE,CD=CF.那么∠EDF=
12、如图,已知:在△ABC中,∠A=80°,BD=BE,CD=CF.那么∠EDF=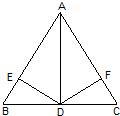 7、如图,已知,在△ABC中,AB=AC,D是BC的中点,DE⊥AB于E,DF⊥AC于F,那么图中全等的三角形有( )对.
7、如图,已知,在△ABC中,AB=AC,D是BC的中点,DE⊥AB于E,DF⊥AC于F,那么图中全等的三角形有( )对.