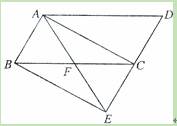
摘要: 如图.将□ABCD的边DC延长到点E.使CE=DC.连接AE.交BC于点F. ⑴求证:△ABF≌△ECF ⑵若∠AFC=2∠D.连接AC.BE.求证:四边形ABEC是矩形. [答案]证明:⑴∵四边形ABCD是平行四边形.∴AB∥CD,AB=CD.∴∠ABF=∠ECF. ∵EC=DC, ∴AB=EC. 在△ABF和△ECF中.∵∠ABF=∠ECF.∠AFB=∠EFC.AB=EC. ∴⊿ABF≌⊿ECF. (2)解法一:∵AB=EC .AB∥EC.∴四边形ABEC是平行四边形.∴AF=EF. BF=CF. ∵四边形ABCD是平行四边形.∴∠ABC=∠D.又∵∠AFC=2∠D.∴∠AFC=2∠ABC. ∵∠AFC=∠ABF+∠BAF.∴∠ABF=∠BAF.∴FA=FB. ∴FA=FE=FB=FC, ∴AE=BC.∴口ABEC是矩形. 解法二:∵AB=EC .AB∥EC.∴四边形ABEC是平行四边形. ∵四边形ABCD是平行四边形.∴AD∥BC.∴∠D=∠BCE. 又∵∠AFC=2∠D.∴∠AFC=2∠BCE. ∵∠AFC=∠FCE+∠FEC.∴∠ FCE=∠FEC.∴∠D=∠FEC.∴AE=AD. 又∵CE=DC.∴AC⊥DE.即∠ACE=90°. ∴口ABEC是矩形.
网址:http://m.1010jiajiao.com/timu3_id_496557[举报]
 (1)在等腰三角形ABC中AB=BC,∠ABC=90°,BD⊥AC,过D点作DE⊥DF,交AB于E,交BC于F.若AE=4,FC=3,求EF长.
(1)在等腰三角形ABC中AB=BC,∠ABC=90°,BD⊥AC,过D点作DE⊥DF,交AB于E,交BC于F.若AE=4,FC=3,求EF长.(2)如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
①求证:△ABF≌△ECF;
②若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.
 21、如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
21、如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
 如图:将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,
如图:将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,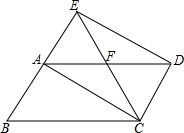 如图,将?ABCD的边BA延长到点E,使AE=AB,连接EC,交AD于点F,连接AC、ED.
如图,将?ABCD的边BA延长到点E,使AE=AB,连接EC,交AD于点F,连接AC、ED.