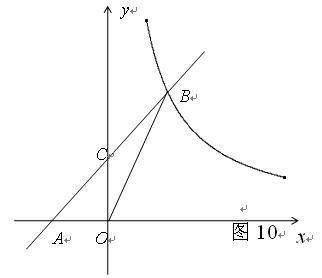
摘要:10. 如图10.在平面直角坐标系xOy中.AB在x轴上.AB=10.以AB为直径的⊙O′与y轴正半轴交于点C.连接BC.AC.CD是⊙O′的切线.AD⊥CD于点D.tan∠CAD=.抛物线过A.B.C三点. (1)求证:∠CAD=∠CAB, (2)①求抛物线的解析式, ②判定抛物线的顶点E是否在直线CD上.并说明理由, (3)在抛物线上是否存在一点P.使四边形PBCA是直角梯形.若存在.直接写出点P的坐标,若不存在.请说明理由. [答案] (1)证明:连接O′C. ∵CD是⊙O′的切线.∴O′C⊥CD··············· 1分 ∵AD⊥CD.∴O′C∥AD.∴∠O′CA=∠CAD··········· 2分 ∵O′C=O′A.∴∠O′CA=∠CAB ∴∠CAD=∠CAB.······················· 3分 (2)∵AB是⊙O′的直径.∴∠ACB=90° ∵OC⊥AB.∴∠CAB=∠OCB.∴△CAO∽△BCO.∴ 即······················ 4分 ∵tan∠CAO=tan∠CAD=.∴OA=2OC 又∵AB=10.∴ ∵OC>0 ∴OC=4.OA=8.OB=2. ∴A.B(2.0).C(0.4)············· 5分 ∵抛物线过A.B.C三点.∴c=4 由题意得.解之得. ∴.···················· 7分 (3)设直线DC交x轴于点F.易证△AOC≌△ADC.∴AD=AO=8. ∵O′C∥AD.∴△FO′C∽△FAD.∴ ∴8(BF+5)=5(BF+10).∴.∴.······ 8分 设直线DC的解析式为.则.即 ∴.······················ 9分 由得 顶点E的坐标为················· 10分 将代入直线DC的解析式中. 右边左边. ∴抛物线的顶点E在直线CD上.··············· 11分 (3)存在..··············· 13分
网址:http://m.1010jiajiao.com/timu3_id_496430[举报]
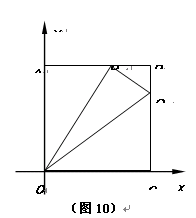
如图10,在平面直角坐标系中,正方形OABC边长是4,点A、C分别在y轴、x轴的正半轴上.动点P从点A开始,以每秒2个单位长度的速度在线段AB上来回运动.动点Q从点B开始沿B→C→O的方向,以每秒1个单位长度的速度向点O运动.P、Q两点同时出发,当点Q到达点O时,P、Q两点同时停止运动.设运动时间为t,△OPQ的面积为S.
(1)当t =1时,S = ;
(2)当0≤ t ≤ 2时,求满足△BPQ的面积有最大值的P、Q两点坐标;
(3)在P、Q两点运动的过程中,是否存在某一时刻,使得S = 6.若存在,请直接写出所有符合条件的P点坐标;若不存在,请说明理由.

查看习题详情和答案>>
 中,直线
中,直线 与
与 轴交于点
轴交于点 ,与反比例函数在第一象限内的图象交于点
,与反比例函数在第一象限内的图象交于点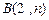 ,连结
,连结 ,若
,若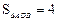 .求该反比例函数的解析式和直线
.求该反比例函数的解析式和直线 式.
式.
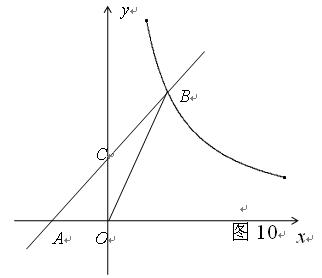
 中,直线
中,直线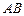 与
与 轴交于点
轴交于点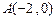 ,与反比例函数在第一象限内的图象交于点
,与反比例函数在第一象限内的图象交于点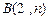 ,连结
,连结 ,若
,若 .求该反比例函数的解析式和直线
.求该反比例函数的解析式和直线