摘要: 如图.等边△ABC内接于⊙O.P是上任一点.连AP.BP.过点C作CM∥BP交PA的延长线于点M. (1)填空:∠APC= 度.∠BPC= 度, (2)求证:△ACM∽△BCP, (3)若PA=1.PB=2.求梯形PBCM的面积. [答案]解:(1)60,60, (2)∵CM∥BP.∴∠BPM+∠M=180°.∠PCM=∠BPC=60. ∴∠M=180°-∠BPM=180-=180°-120°=60°. ∴∠M=∠BPC=60°. (3)∵ACM≌BCP.∴CM=CP.AM=BP. 又∠M=60°.∴△PCM为等边三角形. ∴CM=CP=PM=1+2=3. 作PH⊥CM于H. 在Rt△PMH中.∠MPH=30°. ∴PH=. ∴S梯形PBCM=.
网址:http://m.1010jiajiao.com/timu3_id_496154[举报]
 7、如图,等边△ABC内接于⊙O,以O为旋转中心,能使旋转后的图形与原图形重合.下列符合条件的旋转角是( )
7、如图,等边△ABC内接于⊙O,以O为旋转中心,能使旋转后的图形与原图形重合.下列符合条件的旋转角是( )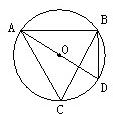 29、如图,等边△ABC内接于⊙O,AD是直径,则∠ADB=
29、如图,等边△ABC内接于⊙O,AD是直径,则∠ADB= 5、如图,等边△ABC内接于⊙O,动点P在劣弧AB上,且不与A、B重合,则∠BPC等于( )
5、如图,等边△ABC内接于⊙O,动点P在劣弧AB上,且不与A、B重合,则∠BPC等于( )
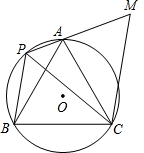 M∥BP交PA的延长线于点M.
M∥BP交PA的延长线于点M. (2011•葫芦岛)如图,等边△ABC内接于⊙O,则∠AOB等于( )
(2011•葫芦岛)如图,等边△ABC内接于⊙O,则∠AOB等于( )