摘要: 如图.AB是⊙O的直径.AC是弦.CD是⊙O的切线.C为切点.AD⊥CD于点D. 求证:(1)∠AOC=2∠ACD, (2)AC2=AB·AD. [答案]证明:(1)∵CD是⊙O的切线.∴∠OCD=90°. 即∠ACD+∠ACO=90°.-① ∵OC=OA.∴∠ACO=∠CAO. ∴∠AOC=180°-2∠ACO.即∠AOC+∠ACO=90°. ② 由①.②.得:∠ACD-∠AOC=0.即∠AOC=2∠ACD, (2)如图.连接BC. ∵AB是直径.∴∠ACB=90°. 在Rt△ACD与△RtACD中. ∵∠AOC=2∠B.∴∠B=∠ACD. ∴△ACD∽△ABC.∴.即AC2=AB·AD.
网址:http://m.1010jiajiao.com/timu3_id_496054[举报]
 如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连结AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连结AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )| A、70° | B、60° | C、50° | D、40° |
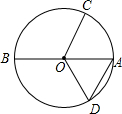 如图,AB是⊙O的直径,点C、D在⊙O上,AD∥OC且∠ODA=55°,则∠BOC等于( )
如图,AB是⊙O的直径,点C、D在⊙O上,AD∥OC且∠ODA=55°,则∠BOC等于( )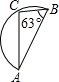 如图,AB是半圆的直径,∠ABC=63°,则
如图,AB是半圆的直径,∠ABC=63°,则
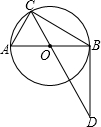 (2013•山西模拟)如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD.已知BC=BD,AB=4.
(2013•山西模拟)如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD.已知BC=BD,AB=4. 如图,AB是⊙O的直径,弦CD⊥AB于点E,连结OC,若OC=5,CD=8,则tan∠COE=( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,连结OC,若OC=5,CD=8,则tan∠COE=( )