网址:http://m.1010jiajiao.com/timu3_id_495989[举报]
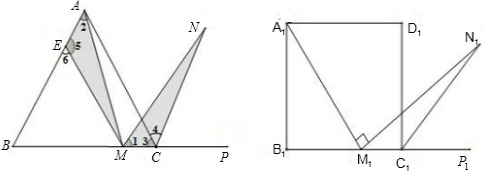
如图1所示,在正三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点.若∠AMN=60°,求证:AM=MN.
(1)经过思考,小明展示了一种正确的证明过程.请你将证明过程补充完整.
证明:在AB上截取EA=MC,连接EM,得△AEM.
∵∠1=180°-∠AMB-∠AMN,∠2=180°-∠AMB-∠B,∠AMN=∠B=60°,∴∠1=∠2.
又CN平分∠ACP,∠4=
| 1 | 2 |
又∵BA=BC,EA=MC,∴BA-EA=BC-MC,即BE=BM.
∴△BEM为等边三角形.∴∠6=60°.
∴∠5=180°-∠6=120°.…②
∴由①②得∠MCN=∠5.
在△AEM和△MCN中,
∵
∴△AEM≌△MCN (ASA).∴AM=MN.
(2)若将试题中的“正三角形ABC”改为“正方形A1B1C1D1”(如图2),N1是∠D1C1P1的平分线上一点,则当∠A1M1N1=90°时,结论A1M1=M1N1.是否还成立?(直接写出答案,不需要证明)
(3)若将题中的“正三角形ABC”改为“正多边形AnBnCnDn…Xn”,请你猜想:当∠AnMnNn=
 查看习题详情和答案>>
查看习题详情和答案>>
数学课堂上,徐老师出示一道试题:
如图(十)所示,在正三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点.若∠AMN=60°,求证:AM=MN.
(1)经过思考,小明展示了一种正确的证明过程.请你将证明过程补充完整.
证明:在AB上截取EA=MC,连结EM,得△AEM.
∵∠1=180°-∠AMB-∠AMN,∠2=180°-∠AMB-∠B,∠AMN=∠B=60°,∴∠1=∠2.
又CN平分∠ACP,∠4=∠ACP=60°.∴∠MCN=∠3+∠4=120°…………①
又∵BA=BC,EA=MC,∴BA-EA=BC-MC,即BE=BM.
∴△BEM为等边三角形.∴∠6=60°.
∴∠5=180°-∠6=120°.………②
∴由①②得∠MCN=∠5.
在△AEM和△MCN中,
∵
∴△AEM≌△MCN (ASA).∴AM=MN.
(2)若将试题中的“正三角形ABC”改为“正方形A1B1C1D1”(如图),N1是∠D1C1P1的平分线上一点,则当∠A1M1N1=90°时,结论A1M1=M1N1.是否还成立?(直接写出答案,不需要证明)
(3) 若将题中的“正三角形ABC”改为“正多边形AnBnCnDn…Xn”,请你猜想:当∠AnMnNn= °时,结论AnMn=MnNn仍然成立?(直接写出答案,不需要证明)


查看习题详情和答案>>
数学课堂上,徐老师出示一道试题:如图(十)所示,在正三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点.若∠AMN=60°,求证:AM=MN.
(1)经过思考,小明展示了一种正确的证明过程.请你将证明过程补充完整.
证明:在AB上截取EA=MC,连结EM,得△AEM.
∵∠1=180°-∠AMB-∠AMN,∠2=180°-∠AMB-∠B,∠AMN=∠B=60°,∴∠1=∠2.
又CN平分∠ACP,∠4=∠ACP=60°.∴∠MCN=∠3+∠4=120°…………①
又∵BA=BC,EA=MC,∴BA-EA=BC-MC,即BE=BM.
∴△BEM为等边三角形.∴∠6=60°.
∴∠5=180°-∠6=120°.………②
∴由①②得∠MCN=∠5.
在△AEM和△MCN中,
∵________________________________
∴△AEM≌△MCN (ASA).∴AM=MN.
(2)若将试题中的“正三角形ABC”改为“正方形A1B1C1D1”(如图),N1是∠D1C1P1的平分线上一点,则当∠A1M1N1=90°时,结论A1M1=M1N1.是否还成立?(直接写出答案,不需要证明)
(3) 若将题中的“正三角形ABC”改为“正多边形AnBnCnDn…Xn”,请你猜想:当∠AnMnNn= °时,结论AnMn=MnNn仍然成立?(直接写出答案,不需要证明)
查看习题详情和答案>>

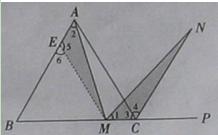
(1)经过思考,小明展示了一种正确的证明过程.请你将证明过程补充完整.
证明:在AB上截取EA=MC,连结EM,得△AEM.
∵∠1=180°-∠AMB-∠AMN,∠2=180°-∠AMB-∠B,∠AMN=∠B=60°,∴∠1=∠2.
又CN平分∠ACP,∠4=∠ACP=60°.∴∠MCN=∠3+∠4=120°…………①
又∵BA=BC,EA=MC,∴BA-EA=BC-MC,即BE=BM.
∴△BEM为等边三角形.∴∠6=60°.
∴∠5=180°-∠6=120°.………②
∴由①②得∠MCN=∠5.
在△AEM和△MCN中,
∵________________________________
∴△AEM≌△MCN (ASA).∴AM=MN.
(2)若将试题中的“正三角形ABC”改为“正方形A1B1C1D1”(如图),N1是∠D1C1P1的平分线上一点,则当∠A1M1N1=90°时,结论A1M1=M1N1.是否还成立?(直接写出答案,不需要证明)
(3)若将题中的“正三角形ABC”改为“正多边形AnBnCnDn…Xn”,请你猜想:当∠AnMnNn= °时,结论AnMn=MnNn仍然成立?(直接写出答案,不需要证明) 查看习题详情和答案>>
如图(十)所示,在正三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点.若∠AMN=60°,求证:AM=MN.
(1)经过思考,小明展示了一种正确的证明过程.请你将证明过程补充完整.
证明:在AB上截取EA=MC,连结EM,得△AEM.
∵∠1=180°-∠AMB-∠AMN,∠2=180°-∠AMB-∠B,∠AMN=∠B=60°,∴∠1=∠2.
又CN平分∠ACP,∠4=∠ACP=60°.∴∠MCN=∠3+∠4=120°…………①
又∵BA=BC,EA=MC,∴BA-EA=BC-MC,即BE=BM.
∴△BEM为等边三角形.∴∠6=60°.
∴∠5=180°-∠6=120°.………②
∴由①②得∠MCN=∠5.
在△AEM和△MCN中,
∵
∴△AEM≌△MCN (ASA).∴AM=MN.
(2)若将试题中的“正三角形ABC”改为“正方形A1B1C1D1”(如图),N1是∠D1C1P1的平分线上一点,则当∠A1M1N1=90°时,结论A1M1=M1N1.是否还成立?(直接写出答案,不需要证明)
(3) 若将题中的“正三角形ABC”改为“正多边形AnBnCnDn…Xn”,请你猜想:当∠AnMnNn= °时,结论AnMn=MnNn仍然成立?(直接写出答案,不需要证明)

 查看习题详情和答案>>
查看习题详情和答案>>