摘要: 设函数 (k为实数). (1)写出其中的两个特殊函数.使它们的图象不全是抛物线.并在同一直角坐标系中.用描点法画出这两个特殊函数的图象, (2)根据所画图象.猜想出:对任意实数K.函数的图象都具有的特征.并给予证明, (3)对任意负实数k.当x<m时.y随着x的增大而增大.试求出m的一个值. [答案](1)当k=1时..当k=0时..图略. (2) 对任意实数k.函数的图象都经过点 证明:把x=-2代入函数.得y=-1.即函数的图象经过点,把x=0代入函数.得y=1.即函数的图象经过点(0.1). (3) 当k为任意负实数.该函数的图象总是开口向下的抛物线.其对称轴为.当负数k所取的值非常小时.正数靠近0.所以靠近-1.所以只要M的值不大于-1即可.
网址:http://m.1010jiajiao.com/timu3_id_495377[举报]
 (2001•黄冈)已知:如图,△ABC中,AB=AC=10,BC=12,F为BC的中点,D是FC上的一点,过点D作BC的垂线交AC于点G,交BA的延长线于点E,如果设DC=x,则
(2001•黄冈)已知:如图,△ABC中,AB=AC=10,BC=12,F为BC的中点,D是FC上的一点,过点D作BC的垂线交AC于点G,交BA的延长线于点E,如果设DC=x,则(1)图中哪些线段(如线段BD可记作yBD)可以看成是x的函数[如yBD=12-x(0<x<6,yFD6-x(0<x<6)]?请再写出其中的四个函数关系式:①
yDG=
x
| 4 |
| 3 |
yDG=
x
;②| 4 |
| 3 |
yGC=
x
| 5 |
| 3 |
yGC=
x
;③| 5 |
| 3 |
yAG=-
x+10
| 5 |
| 3 |
yAG=-
x+10
;④| 5 |
| 3 |
yAE=
(6-x)=-
x+10
| 5 |
| 3 |
| 5 |
| 3 |
yAE=
(6-x)=-
x+10
.| 5 |
| 3 |
| 5 |
| 3 |
(2)图中哪些图形的面积(如△CDG的面积可记作S△CDG)可以看成是x的函数[如S△CDG=
| 2 |
| 3 |
S△BDE=
(12-x)2=
x2-16x+96
| 2 |
| 3 |
| 2 |
| 3 |
S△BDE=
(12-x)2=
x2-16x+96
;②| 2 |
| 3 |
| 2 |
| 3 |
S四边形AGDF=
(36-x2)=-
x2+24
| 2 |
| 3 |
| 2 |
| 3 |
S四边形AGDF=
(36-x2)=-
x2+24
.| 2 |
| 3 |
| 2 |
| 3 |
设函数y=kx2+(2k+1)x+1(k为实数)
(1)写出其中的两个特殊函数,使它们的图象不全是抛物线,并在同一直角坐标系中,用描点法画出这两个特殊函数的图象;
(2)根据所画图象,猜想出:对任意实数k,函数的图象都具有的特征,并给予证明;
(3)对任意负实数k,当x<m时,y随着x的增大而增大,试求出m的一个值. 查看习题详情和答案>>
(1)写出其中的两个特殊函数,使它们的图象不全是抛物线,并在同一直角坐标系中,用描点法画出这两个特殊函数的图象;
(2)根据所画图象,猜想出:对任意实数k,函数的图象都具有的特征,并给予证明;
(3)对任意负实数k,当x<m时,y随着x的增大而增大,试求出m的一个值. 查看习题详情和答案>>
(本小题满分10分)设函数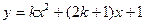 (
(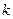 为实数)
为实数)
(1)写出其中的两个特殊函数,使它们的图像不全是抛物线,并在同一直角坐标系中,用描点法画出这两个特殊函数的图像;
(2)根据所画图像,猜想出:对任意实数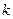 ,函数的图像都具有的特征,并给予证明;
,函数的图像都具有的特征,并给予证明;
(3)对任意负实数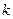 ,当
,当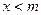 时,
时,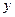 随着
随着 的增大而增大,试求出
的增大而增大,试求出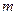 的一个值
查看习题详情和答案>>
的一个值
查看习题详情和答案>>
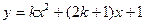 (
(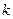 为实数)
为实数)(1)写出其中的两个特殊函数,使它们的图像不全是抛物线,并在同一直角坐标系中,用描点法画出这两个特殊函数的图像;
(2)根据所画图像,猜想出:对任意实数
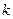 ,函数的图像都具有的特征,并给予证明;
,函数的图像都具有的特征,并给予证明;(3)对任意负实数
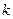 ,当
,当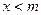 时,
时,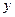 随着
随着 的增大而增大,试求出
的增大而增大,试求出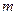 的一个值
查看习题详情和答案>>
的一个值
查看习题详情和答案>>