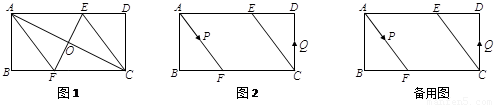摘要: 已知,矩形中,,, 的垂直平分线分别交.于点.,垂足为. (1)如图10-1,连接..求证四边形为菱形,并求的长, (2)如图10-2,动点.分别从.两点同时出发,沿和各边匀速运动一周.即点自→→→停止,点自→→→停止.在运动过程中, ①已知点的速度为每秒5,点的速度为每秒4,运动时间为秒,当...四点为顶点的四边形是平行四边形时,求的值. ②若点.的运动路程分别为.(单位:,),已知...四点为顶点的四边形是平行四边形,求与满足的数量关系式. [答案](1)证明:①∵四边形是矩形 ∴∥ ∴, ∵垂直平分,垂足为 ∴ ∴≌ ∴ ∴四边形为平行四边形 又∵ ∴四边形为菱形 ②设菱形的边长,则 在中, 由勾股定理得,解得 ∴ (2)①显然当点在上时,点在上,此时...四点不可能构成平行四边形;同理点在上时,点在或上,也不能构成平行四边形.因此只有当点在上.点在上时,才能构成平行四边形 ∴以...四点为顶点的四边形是平行四边形时, ∵点的速度为每秒5,点的速度为每秒4,运动时间为秒 ∴, ∴,解得 ∴以...四点为顶点的四边形是平行四边形时,秒. ②由题意得,以...四点为顶点的四边形是平行四边形时,点.在互相平行的对应边上. 分三种情况: i)如图1,当点在上.点在上时,,即,得 ii)如图2,当点在上.点在上时,, 即,得 iii)如图3,当点在上.点在上时,,即,得 综上所述,与满足的数量关系式是
网址:http://m.1010jiajiao.com/timu3_id_495298[举报]
(10分) 已知,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,垂足为
,垂足为![]() .
.
1.(1)如图1,连接![]() 、
、![]() .求证四边形
.求证四边形![]() 为菱形,并求
为菱形,并求![]() 的长;
的长;
2.(2)如图2,动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时出发,沿
两点同时出发,沿![]() 和
和![]() 各边匀速运动一周.即点
各边匀速运动一周.即点![]() 自
自![]() →
→![]() →
→![]() →
→![]() 停止,点
停止,点![]() 自
自![]() →
→![]() →
→![]() →
→![]() 停止.在运动过程中,
停止.在运动过程中,
①已知点![]() 的速度为每秒5
的速度为每秒5![]() ,点
,点![]() 的速度为每秒4
的速度为每秒4![]() ,运动时间为
,运动时间为![]() 秒,当
秒,当![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形时,求
四点为顶点的四边形是平行四边形时,求![]() 的值.
的值.
②若点![]() 、
、![]() 的运动路程分别为
的运动路程分别为![]() 、
、![]() (单位:
(单位:![]() ,
,![]() ),已知
),已知![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形,求
四点为顶点的四边形是平行四边形,求![]() 与
与![]() 满足的数量关系式.
满足的数量关系式.
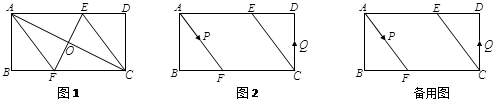
查看习题详情和答案>>
(12分)已知,矩形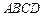 中,
中,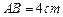 ,
, ,
, 的垂直平分线
的垂直平分线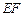 分别交
分别交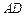 、
、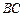 于点
于点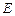 、
、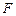 ,垂足为
,垂足为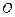 .
.
(1)如图10-1,连接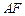 、
、 .求证四边形
.求证四边形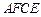 为菱形,并求
为菱形,并求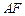 的长;
的长;
(2)如图10-2,动点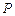 、
、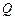 分别从
分别从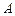 、
、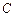 两点同时出发,沿
两点同时出发,沿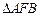 和
和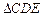 各边匀速运动一周.即点
各边匀速运动一周.即点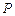 自
自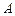 →
→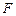 →
→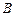 →
→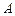 停止,点
停止,点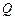 自
自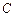 →
→ →
→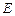 →
→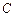 停止.在运动过程中,
停止.在运动过程中,
①已知点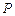 的速度为每秒5
的速度为每秒5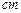 ,点
,点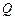 的速度为每秒4
的速度为每秒4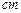 ,运动时间为
,运动时间为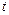 秒,当
秒,当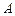 、
、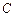 、
、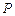 、
、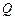 四点为顶点的四边形是平行四边形时,求
四点为顶点的四边形是平行四边形时,求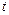 的值.
的值.
②若点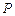 、
、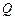 的运动路程分别为
的运动路程分别为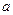 、
、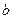 (单位:
(单位: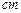 ,
,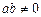 ),已知
),已知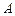 、
、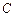 、
、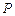 、
、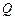 四点为顶点的四边形是平行四边形,求
四点为顶点的四边形是平行四边形,求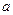 与
与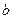 满足的数量关系式.
满足的数量关系式. 查看习题详情和答案>>
查看习题详情和答案>>
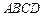 中,
中,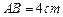 ,
, ,
, 的垂直平分线
的垂直平分线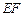 分别交
分别交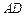 、
、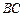 于点
于点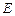 、
、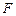 ,垂足为
,垂足为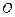 .
.(1)如图10-1,连接
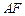 、
、 .求证四边形
.求证四边形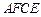 为菱形,并求
为菱形,并求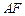 的长;
的长;(2)如图10-2,动点
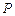 、
、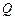 分别从
分别从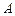 、
、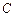 两点同时出发,沿
两点同时出发,沿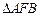 和
和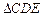 各边匀速运动一周.即点
各边匀速运动一周.即点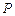 自
自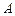 →
→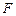 →
→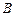 →
→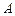 停止,点
停止,点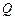 自
自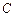 →
→ →
→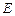 →
→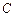 停止.在运动过程中,
停止.在运动过程中,①已知点
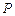 的速度为每秒5
的速度为每秒5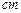 ,点
,点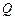 的速度为每秒4
的速度为每秒4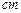 ,运动时间为
,运动时间为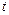 秒,当
秒,当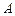 、
、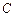 、
、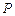 、
、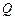 四点为顶点的四边形是平行四边形时,求
四点为顶点的四边形是平行四边形时,求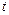 的值.
的值.②若点
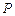 、
、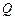 的运动路程分别为
的运动路程分别为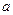 、
、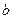 (单位:
(单位: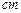 ,
,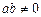 ),已知
),已知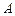 、
、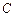 、
、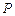 、
、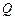 四点为顶点的四边形是平行四边形,求
四点为顶点的四边形是平行四边形,求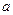 与
与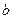 满足的数量关系式.
满足的数量关系式. 查看习题详情和答案>>
查看习题详情和答案>>
已知,矩形 中,
中, ,
,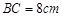 ,
,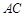 的垂直平分线
的垂直平分线 分别交
分别交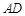 、
、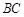 于点
于点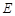 、
、 ,垂足为
,垂足为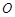 .
.
(1)如图1,连接 、
、 .求证四边形
.求证四边形 为菱形,并求
为菱形,并求 的长;
的长;
(2)如图2,动点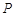 、
、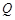 分别从
分别从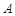 、
、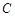 两点同时出发,沿
两点同时出发,沿 和
和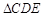 各边匀速运动一周.即点
各边匀速运动一周.即点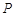 自
自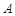 →
→ →
→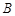 →
→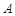 停止,点
停止,点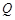 自
自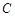 →
→ →
→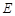 →
→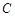 停止.在运动过程中,已知点
停止.在运动过程中,已知点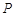 的速度为每秒5
的速度为每秒5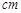 ,点
,点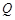 的速度为每秒4
的速度为每秒4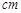 ,运动时间为
,运动时间为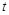 秒,当
秒,当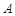 、
、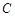 、
、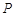 、
、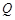 四点为顶点的四边形是平行四边形时,求
四点为顶点的四边形是平行四边形时,求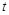 的值.
的值.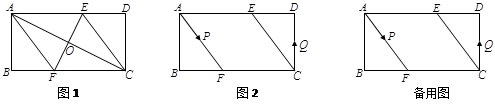
 中,
中, ,
,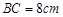 ,
,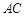 的垂直平分线
的垂直平分线 分别交
分别交 、
、 于点
于点 、
、 ,垂足为
,垂足为 .
. 、
、 .求证四边形
.求证四边形 为菱形,并求
为菱形,并求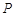 、
、 分别从
分别从 、
、 两点同时出发,沿
两点同时出发,沿 和
和 各边匀速运动一周.即点
各边匀速运动一周.即点 →
→ →
→ ,点
,点 秒,当
秒,当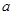 、
、 (单位:
(单位: ),已知
),已知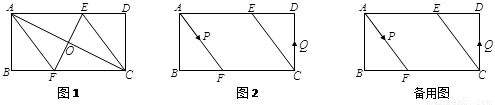
 中,
中,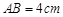 ,
,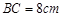 ,
,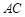 的垂直平分线
的垂直平分线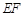 分别交
分别交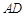 、
、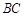 于点
于点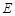 、
、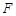 ,垂足为
,垂足为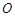 .
.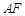 、
、 .求证四边形
.求证四边形 为菱形,并求
为菱形,并求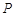 、
、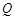 分别从
分别从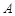 、
、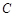 两点同时出发,沿
两点同时出发,沿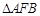 和
和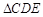 各边匀速运动一周.即点
各边匀速运动一周.即点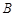 →
→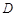 →
→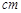 ,点
,点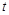 秒,当
秒,当