摘要:在平面直角坐标系中.直线(k为常数且k≠0)分别交x轴.y轴于点A.B.⊙O半径为个单位长度. ⑴如图甲.若点A在x轴正半轴上.点B在y轴正半轴上.且OA=OB. ①求k的值, ②若b=4.点P为直线上的动点.过点P作⊙O的切线PC.PD.切点分别为C.D.当PC⊥PD时.求点P的坐标. ⑵若.直线将圆周分成两段弧长之比为1∶2.求b的值. [分析]⑴①由OA=OB=b .不难求得k的值,②过P作x轴的垂线.设法求出点P到x轴与y轴的距离,⑵直线将圆周分成两段弧长之比为1∶2.可知其所对圆心角为120°.直线中∴直线与x轴交角的正切值为.充分理解这两层意思.再结合直角三角形将直线所经过的某一点的坐标求出.即得其解析式. [答案]⑴①根据题意得:B的坐标为(0.b).∴OA=OB=b.∴A的坐标为(b.0).代入y=kx+b得k=-1. ②过P作x轴的垂线.垂足为F.连结OD. ∵PC.PD是⊙O的两条切线.∠CPD=90°. ∴∠OPD=∠OPC=∠CPD=45°. ∵∠PDO=90°..∠POD=∠OPD=45°. ∴OD=PD=.OP=. ∵P在直线y=-x+4上.设P(m.-m+4).则OF=m.PF=-m+4. ∵∠PFO=90°. OF2+PF2=PO2. ∴ m2+ (-m+4)2=()2. 解得m=1或3. ∴P的坐标为 ⑵分两种情形.y=-x+.或y=-x-. 直线将圆周分成两段弧长之比为1∶2.可知其所对圆心角为120°.如图.画出弦心距OC.可得弦心距OC=.又∵直线中∴直线与x轴交角的正切值为.即.∴AC=.进而可得AO=.即直线与与x轴交于点(.0).所以直线与y轴交于点(.0).所以b的值为. 当直线与x轴.y轴的负半轴相交.同理可求得b的值为. 综合以上得:b的值为或. [涉及知识点]一次函数.勾股定理.圆的切线等知识的综合运用 [点评]中考题的最后一两道题俗称压轴题.主要考查学生的综合运用能力.包括知识综合.方法综合以及数学思想的综合运用.能较好地区分出不同数学水平的学生.保证区分结果的稳定性.从而确保试题具有良好的区分度.进而有利于高一级学校选拔新生.对我们学生而言要注意从简单的地方入手.将一些数学语言用自己熟悉的便于理解的即换一种语言表达出来.这些方法对解答综合题有一定的作用. [推荐指数]★★★★
网址:http://m.1010jiajiao.com/timu3_id_495140[举报]
 10、在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
10、在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;
(2)如果点P的坐标是(-a,0),其中a>0,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.
 (2013•温州)如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴上的一动点,连接CD,DE,以CD,DE为边作?CDEF.
(2013•温州)如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴上的一动点,连接CD,DE,以CD,DE为边作?CDEF.(1)当0<m<8时,求CE的长(用含m的代数式表示);
(2)当m=3时,是否存在点D,使?CDEF的顶点F恰好落在y轴上?若存在,求出点D的坐标;若不存在,请说明理由;
(3)点D在整个运动过程中,若存在唯一的位置,使得?CDEF为矩形,请求出所有满足条件的m的值.
 如图,在平面直角坐标系中,直线y=kx+2与x轴交于点A,与y轴交于点B,与抛物线y=ax2+bx交于点C、D.已知点C的坐标为(2,1),点D的横坐标为
如图,在平面直角坐标系中,直线y=kx+2与x轴交于点A,与y轴交于点B,与抛物线y=ax2+bx交于点C、D.已知点C的坐标为(2,1),点D的横坐标为| 1 | 2 |
(1)求点D的坐标;
(2)求抛物线的函数表达式;
(3)抛物线在x轴上方部分是否存在一点P,使△POA的面积比△POB的面积大4?如果存在,求出点P的坐标;如果不存在,说明理由.
(4)将题中的抛物线y=ax2+bx沿x轴平移,当抛物线经过点B时,请直接写出平移的方向和距离.
 如图,在平面直角坐标系中,直线
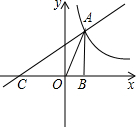
如图,在平面直角坐标系中,直线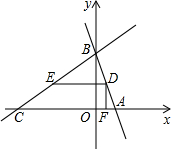 在 平面直角坐标系中,直线y=-3x+3与x轴交于点A,与y轴交于点B,以B为顶点作∠CBA=∠CAB交x轴负半轴于点C.
在 平面直角坐标系中,直线y=-3x+3与x轴交于点A,与y轴交于点B,以B为顶点作∠CBA=∠CAB交x轴负半轴于点C.