摘要:27.如图.二次函数的图象经过点D.与x轴交于A.B两点. ⑴求的值, ⑵如图①.设点C为该二次函数的图象在x轴上方的一点.直线AC将四边形ABCD的面积二等分.试证明线段BD被直线AC平分.并求此时直线AC的函数解析式, ⑶设点P.Q为该二次函数的图象在x轴上方的两个动点.试猜想:是否存在这样的点P.Q.使△AQP≌△ABP?如果存在.请举例验证你的猜想,如果不存在.请说明理由. [分析]⑴将D点坐标代入二次函数解析式即可求出c的值,⑵要证明线段BD被直线AC平分.从“直线AC将四边形ABCD的面积二等分 来录求解题思路.不难发现S△ABC=S△ADC.通过面积法可得AC公共边上的两条高相等.再通过全等可得线段BD被直线AC平分,⑶通过逆向思考.假设存在这样的点P.Q.使△AQP≌△ABP.则可得AP平分∠QAB.通过画图可进一步确认其存在的可能性. [答案]⑴ ∵抛物线经过点D() ∴ ∴c=6. ⑵过点D.B点分别作AC的垂线.垂足分别为E.F.设AC与BD交点为M. ∵AC 将四边形ABCD的面积二等分.即:S△ABC=S△ADC ∴DE=BF 又∵∠DME=∠BMF. ∠DEM=∠BFE ∴△DEM≌△BFM ∴DM=BM 即AC平分BD ∵c=6. ∵抛物线为 ∴A().B() ∵M是BD的中点 ∴M() 设AC的解析式为y=kx+b.经过A.M点 解得 直线AC的解析式为. ⑶存在.设抛物线顶点为N(0.6).在Rt△AQN中.易得AN=.于是以A点为圆心.AB=为半径作圆与抛物线在x上方一定有交点Q.连接AQ.再作∠QAB平分线AP交抛物线于P.连接BP.PQ.此时由“边角边 易得△AQP≌△ABP. [涉及知识点]二次函数.一次函数.解直角三角形及其知识的综合运用 [点评]一道题能涉及众多重点知识.既有代数的.又有几何的.又能考查到重要的数学思想.方法.这正是代数几何综合题的“本色 .综合性强.能力要求高.区分度大.决定了代数几何综合题历来被命题者所看重.从近几年的中考来看.不少试卷把其作为压轴题把关.在复习中要对这类问题引起足够重视.掌握这类问题的几种典型类型.加强这类问题的训练. [推荐指数]★★★★
网址:http://m.1010jiajiao.com/timu3_id_495139[举报]
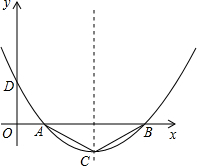 如图,二次函数的图象经过点D(0,
如图,二次函数的图象经过点D(0,| 7 |
| 9 |
| 3 |
(1)求二次函数的解析式;
(2)在该抛物线的对称轴上找一点P,使PA+PD最小,求出点P的坐标;
(3)在抛物线上是否存在点Q,使△QAB与△ABC相似?如果存在,求出点Q的坐标;如果不存在,请说明理由. 查看习题详情和答案>>
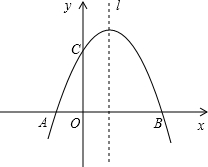 已知:如图,二次函数的图象是由y=-x2向右平移1个单位,再向上平移4个单位所得到.
已知:如图,二次函数的图象是由y=-x2向右平移1个单位,再向上平移4个单位所得到.(1)求二次函数的解析式;
(2)若点P是抛物线对称轴l上一动点,求使AP+CP最小的点P的坐标.
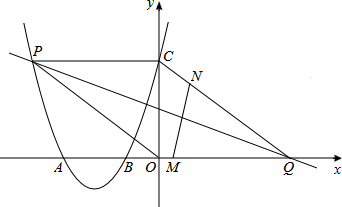
(2013•海南)如图,二次函数的图象与x轴相交于点A(-3,0)、B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx-4k(k≠0)的图象过点P交x轴于点Q.
(1)求该二次函数的解析式;
(2)当点P的坐标为(-4,m)时,求证:∠OPC=∠AQC;
(3)点M,N分别在线段AQ、CQ上,点M以每秒3个单位长度的速度从点A向点Q运动,同时,点N以每秒1个单位长度的速度从点C向点Q运动,当点M,N中有一点到达Q点时,两点同时停止运动,设运动时间为t秒.连接AN,当△AMN的面积最大时,
①连接AN,当△AMN的面积最大时,求t的值;
②线段PQ能否垂直平分线段MN?若能,请求出此时点P的坐标;若不能,请说明你的理由.
查看习题详情和答案>>
(1)求该二次函数的解析式;
(2)当点P的坐标为(-4,m)时,求证:∠OPC=∠AQC;
(3)点M,N分别在线段AQ、CQ上,点M以每秒3个单位长度的速度从点A向点Q运动,同时,点N以每秒1个单位长度的速度从点C向点Q运动,当点M,N中有一点到达Q点时,两点同时停止运动,设运动时间为t秒.连接AN,当△AMN的面积最大时,
①连接AN,当△AMN的面积最大时,求t的值;
②线段PQ能否垂直平分线段MN?若能,请求出此时点P的坐标;若不能,请说明你的理由.

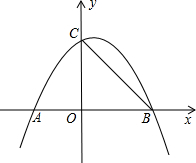 如图,二次函数的图象与x轴相交于A、B两点,与y轴相交于点C.且OA=2,OC=OB=3.
如图,二次函数的图象与x轴相交于A、B两点,与y轴相交于点C.且OA=2,OC=OB=3.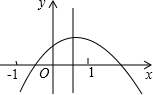 已知,如图:二次函数的图象如图所示,给出以下结论:
已知,如图:二次函数的图象如图所示,给出以下结论: