摘要:如图.四边形ABCD是矩形.∠EDC=∠CAB.∠DEC=90°. (1)求证:AC∥DE, (2)过点B作BF⊥AC于点F.连结EF.试判断四边形BCEF的形状.并说明理由. [分析](1)要证AC∥DE.设法证两个内错角相等.由已知∠EDC=∠CAB.再由矩形利用两边平行将∠ACD作为中间量进行转化,(2)可先猜想四边形BCEF是平行四边形.设法证EF.BC与AD的关系运用EF.BC平行且相等可得证. [答案]⑴在矩形ABCD中.AC∥DE.∴∠DCA=∠CAB.∵∠EDC=∠CAB. ∴∠DCA=∠EDC.∴AC∥DE, ⑵四边形BCEF是平行四边形. 理由:由∠DEC=90°.BF⊥AC.可得∠AFB=∠DEC=90°. 又∠EDC=∠CAB.AB=CD. ∴△DEC≌△AFB.∴DE=AF.由⑴得AC∥DE. ∴四边形AFED是平行四边形.∴AD∥EF且AD=EF. ∵在矩形ABCD中.AD∥BC且AD=BC. ∴EF∥BC且EF=BC. ∴四边形BCEF是平行四边形. [涉及知识点]矩形的性质 平行四边形的判定 全等三角形的判定 [点评]从中考试卷来看.平行四边形这一节不会有很复杂的证明题.主要考查平行四边形的性质特征及判别方法综合运用. 掌握这部分内容.首先搞清平行四边形与矩形.菱形. 正方形之间的包含关系.注重把握特殊平行四边形与一般平行四边形的异.同点.才能准确地.灵活地运用. [推荐指数]★★★★★
网址:http://m.1010jiajiao.com/timu3_id_495134[举报]
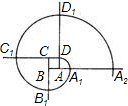 如图,四边形ABCD是正方形,曲线DA1B1C1D1…叫做“正方形的渐开线”,其中曲线DA1、A1B1、B1C1、C1D1、…的圆心依次按A、B、C、D循环,它们依次连接.取AB=1,则曲线DA1B1…C2D2的长是
如图,四边形ABCD是正方形,曲线DA1B1C1D1…叫做“正方形的渐开线”,其中曲线DA1、A1B1、B1C1、C1D1、…的圆心依次按A、B、C、D循环,它们依次连接.取AB=1,则曲线DA1B1…C2D2的长是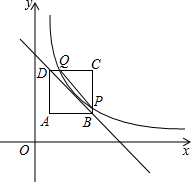 (2012•葫芦岛)如图,四边形ABCD是正方形,其中A(1,1),B(3,1),D(1,3).反比例函数y=
(2012•葫芦岛)如图,四边形ABCD是正方形,其中A(1,1),B(3,1),D(1,3).反比例函数y=| m | x |
(1)直接写出点M,C的坐标;
(2)求直线BD的解析式;
(3)线段PQ与BD是否平行?并说明理由.
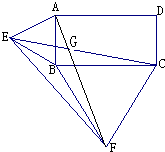 16、如图,四边形ABCD是矩形,△ABE和△BCF都是等边三角形,且点E、F都在矩形外.
16、如图,四边形ABCD是矩形,△ABE和△BCF都是等边三角形,且点E、F都在矩形外.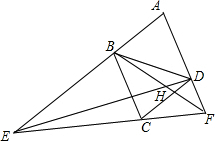 已知:如图,四边形ABCD是菱形,∠A=60°,直线EF经过点C,分别交AB、AD的延长线于E、F两点,连接ED、FB相交于点H.
已知:如图,四边形ABCD是菱形,∠A=60°,直线EF经过点C,分别交AB、AD的延长线于E、F两点,连接ED、FB相交于点H.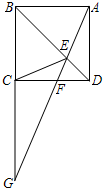 如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F.求证:四边形ABCD是正方形.
如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F.求证:四边形ABCD是正方形.