摘要：(2010江苏泰州.19⑴.8分)计算: (1), [分析]根据零指数幂与负整指数幂即:a0＝1(a≠0).(a≠0)可得=-2.=1.由特殊锐角三角函数值可知.再化简二次根式． [答案]原式===． [涉及知识点]实数的混合运算 零指数幂与负整指数幂 特殊锐角三角函数值 二次根式的化简 [点评]实数的混合运算首先注意运算顺序.其次运算律的灵活运用.最后是掌握幂的运算性质.特殊锐角三角函数值.二次根式的化简等知识点． [推荐指数]★★★ (2010江苏泰州.19⑵.8分)(2)． [分析]先对括号内的两个分式通分.最简公分母是a(a+2).再做除法.最后做加减． [答案]原式=== ===． [涉及知识点]分式的加减乘除混合运算 [点评]分式的混合运算.要牢记运算法则和运算顺序.并能灵活应用.分式的运算结果应是最简分式或整式．这里要强调一下.在进行分式通分后.根据分式加减法法则进行分式的加减运算.是分母不变.把分子相加减.有些同学生容易受解分式方程去分母这一步的影响.同时把分母去掉了.要引起重视.不能相混淆． [推荐指数]★★★★
网址：http://m.1010jiajiao.com/timu3_id_495131[举报]
某中学开展“五比五创”演讲比赛活动，九（1）班准备根据根据平时练习成绩准备从张华、李明2名选手选出一名参加比赛，他们两人的五次平时成绩（满分20分）如图所示．（1）根据如图，分别求出张华、李明的平均成绩和方差；
（2）根据（1）的计算结果，分析张华、李明同学各自的优点，并决定让那位同学参加比赛？
21、某中学开展演讲比赛活动，九（1）、九（2）班根据初赛成绩各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如图所示．（1）根据右图，分别求出两班复赛的平均成绩和方差；
（2）根据（1）的计算结果，分析哪个班级的复赛成绩比较稳定．
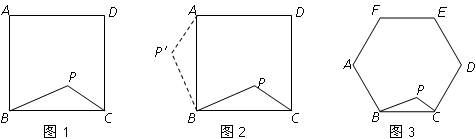
【问题】如图17-1，在正方形ABCD内有一点P，PA=
，PB=
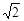，PC=1，求∠BPC的度数．
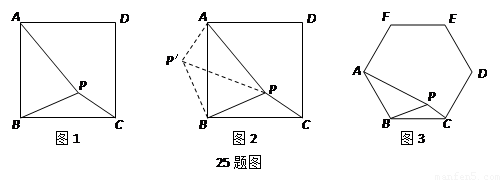
分析根据已知条件比较分散的特点，我们可以通过旋转变换将分散的已知条件集中在一起，于是将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图17-2），然后连结PP′．
解决问题请你通过计算求出图17-2中∠BPC的度数；
类比研究 如图17-3，若在正六边形ABCDEF内有一点P，且PA=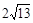
，PB=4，PC=2.
（1）∠BPC的度数为 ； （2）直接写出正六边形ABCDEF的边长为 ．
查看习题详情和答案>>
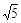，PB=
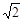，PC=1，求∠BPC的度数．
，PB=4，PC=2.