摘要:23.如图1.在等边△ABC中.点D是边AC的中点.点P是线段DC上的动点(点P与点C不重合).连结BP. 将△ABP绕点P按顺时针方向旋转α角(0°<α<180°).得到△A1B1P,连结AA1.射线AA1分别交射线PB.射线B1B于点E.F. (1) 如图1.当0°<α<60°时.在α角变化过程中.△BEF与△AEP始终存在 ▲ 关系.并说明理由, (2)如图2.设∠ABP=β . 当60°<α<180°时.在α角变化过程中.是否存在△BEF与△AEP全等?若存在.求出α与β之间的数量关系,若不存在.请说明理由, (3)如图3.当α=60°时.点E.F与点B重合. 已知AB=4.设DP=x.△A1BB1的面 积为S.求S关于x的函数关系式.
网址:http://m.1010jiajiao.com/timu3_id_494002[举报]
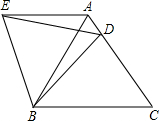
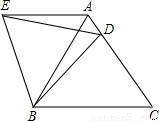
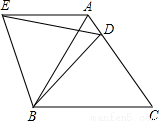
 如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=10,BD=9,则△AED的周长是________.
如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=10,BD=9,则△AED的周长是________.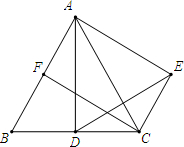 如图,在等边△ABC中,点D是BC边的中点,将△ADC沿AC边翻折得到△AEC,连接DE.
如图,在等边△ABC中,点D是BC边的中点,将△ADC沿AC边翻折得到△AEC,连接DE.