网址:http://m.1010jiajiao.com/timu3_id_492562[举报]
如图,在梯形ABCD中,AB∥DC,∠ABC=90°,AB=2,BC=4,tan∠ADC=2.
(1)求证:DC=BC;
(2)E是梯形内一点,连接DE、CE,将△DCE绕点C顺时针旋转90°,得△BCF,连接EF.判断EF与CE的数量关系,并证明你的结论;
(3)在(2)的条件下,当CE=2BE,∠BEC=135°时,求cos∠BFE的值.
如图,在梯形ABCD中,AB∥DC,∠ABC=90°,AB=2,BC=4,tan∠ADC=2.
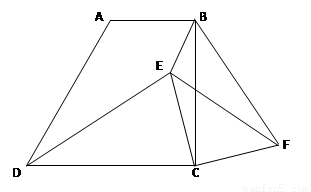
(1)求证:DC=BC;
(2)E是梯形内一点,连接DE、CE,将△DCE绕点C顺时针旋转90°,得△BCF,连接EF.判断EF与CE的数量关系,并证明你的结论;
(3)在(2)的条件下,当CE=2BE,∠BEC=135°时,求cos∠BFE的值.
查看习题详情和答案>>

(1)求证:DC=BC;
(2)E是梯形内一点,连接DE、CE,将△DCE绕点C顺时针旋转90°,得△BCF,连接EF.判断EF与CE的数量关系,并证明你的结论;
(3)在(2)的条件下,当CE=2BE,∠BEC=135°时,求cos∠BFE的值.
如图,在梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°,AB=30,BC=x(15<x<30).作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.

(1)用含有x的代数式表示BF的长.
(2)设四边形DEBG的面积为S,求S与x的函数关系式.
(3)当x为何值时,S有最大值,并求出这个最大值.
如图①,在梯形ABCD中,CD∥AB,∠ABC=90°,∠DAB=60°,AD=2,CD=4.另有一直角三角形EFG,∠EFG=90°,点G与点E重合,点E与点A重合,点F在AB上,让△EFG的边EF在AB上,点G在DC上,以每秒1个单位的速度沿着AB方向向右运动,如图②,点F与点B重合时停止运动,设运动时间为t秒.
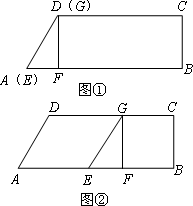
(1)在上述运动过程中,请分别写出当四边形FBCG为正方形和四边形AEGD为平行四边形时对应时刻t的值或范围;
(2)以点A为原点,以AB所在直线为x轴,过点A垂直于AB的直线为y轴,建立如图所示的坐标系.求过A,D,C三点的抛物线的解析式;
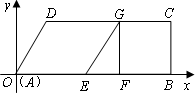
(3)探究:延长EG交(2)中的抛物线于点Q,是否存在这样的时刻t使得△ABQ的面积与梯形ABCD的面积相等?若存在,求出t的值;若不存在,请说明理由.