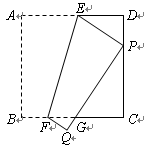
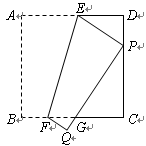
摘要：18．已知:点F在正方形纸片ABCD的边CD上.AB=2.∠FBC=30°,沿BF折叠纸片.使点C落在纸片内点C＇处,再继续以BC＇为轴折叠纸片.把点A落在纸片上的位置记作A＇.则点D和A＇之间的距离为 .
网址：http://m.1010jiajiao.com/timu3_id_492020[举报]
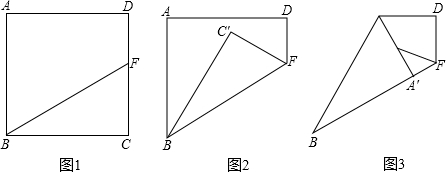
已知：点F在正方形纸片ABCD的边CD上，AB=2，∠FBC=30°（如图1）；沿BF折叠纸片，使点C落在纸片内点C′处（如图2）；再继续以BC′为轴折叠纸片，把点A落在纸片上的位置记作A′（如图3），则点D和A′之间的距离为 ．
查看习题详情和答案>>
查看习题详情和答案>>
已知正方形纸片ABCD的边长为2．如图，将正方形纸片折叠，使顶点A落在边CD上的点P处（点P与C、D不重合），折痕为EF，折叠后AB边落在PQ的位置，PQ与BC交于点G．
（1）求证：△DEP与△CPG相似；
（2）当点P位于CD中点时，求：△DEP与△CPG周长的比；
（3）在（2）的条件下，求证：以P为圆心，以1为半径的圆与直线EG相切．
查看习题详情和答案>>
（1）求证：△DEP与△CPG相似；
（2）当点P位于CD中点时，求：△DEP与△CPG周长的比；
（3）在（2）的条件下，求证：以P为圆心，以1为半径的圆与直线EG相切．
已知正方形纸片ABCD的边长为2．
操作：如图1，将正方形纸片折叠，使顶点A落在边CD上的点P处(点P与C、D不重合)，折痕为EF，折叠后AB边落在PQ的位置，PQ与BC交于点G．
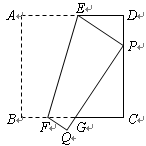
探究：1.(1)观察操作结果，找到一个与△DEP相似的三角形，并证明你的结论；
2.(2)当点P位于CD中点时，你找到的三角形与△DEP周长的比是多少？
查看习题详情和答案>>
