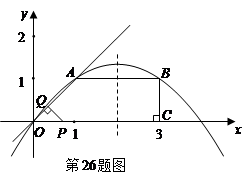摘要:如图所示.已知在直角梯形中.轴于点.动点从点出发.沿轴正方向以每秒1个单位长度的速度移动.过点作垂直于直线.垂足为.设点移动的时间为秒().与直角梯形重叠部分的面积为. (1)求经过三点的抛物线解析式, (2)求与的函数关系式, (3)将绕着点顺时针旋转.是否存在.使得的顶点或在抛物线上?若存在.直接写出的值,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu3_id_491632[举报]
如图所示,已知在直角梯形![]() 中,
中,![]() 轴于点
轴于点![]() .动点
.动点![]() 从
从![]() 点出发,沿
点出发,沿![]() 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过![]() 点作
点作![]() 垂直于直线
垂直于直线![]() ,垂足为
,垂足为![]() .设
.设![]() 点移动的时间为
点移动的时间为![]() 秒(
秒(![]() ),
),![]() 与直角梯形
与直角梯形![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
(1)求经过![]() 三点的抛物线解析式;
三点的抛物线解析式;
(2)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,是否存在
,是否存在![]() ,使得
,使得![]() 的顶点
的顶点![]() 或
或![]() 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 |
查看习题详情和答案>>
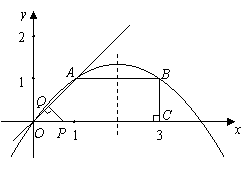
如图所示,已知在直角梯形![]() 中,
中,![]() 轴于点
轴于点![]() .动点
.动点![]() 从
从![]() 点出发,沿
点出发,沿![]() 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过![]() 点作
点作![]() 垂直于直线
垂直于直线![]() ,垂足为
,垂足为![]() .设
.设![]() 点移动的时间为
点移动的时间为![]() 秒(
秒(![]() ),
),![]() 与直角梯形
与直角梯形![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
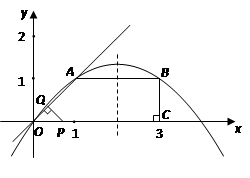
(1)求经过![]() 三点的抛物线解析式;
三点的抛物线解析式;
(2)将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,是否存在
,是否存在![]() ,使得
,使得![]() 的顶点
的顶点![]() 或
或![]() 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)求![]() 与
与![]() 的函数关系式.
的函数关系式.
【解析】(1)设抛物线解析式为y=ax2+bx,把已知坐标代入求出抛物线的解析式(2)根据旋转的性质,代入解析式,判断是否存在(3)求出S的面积,根据t的取值不同分三种情况讨论S与t的函数关系式
查看习题详情和答案>>
如图所示,已知在直角梯形![]() 中,
中,![]() 轴于点
轴于点
 .动点
.动点 从
从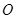 点出发,沿
点出发,沿 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过 点作
点作 垂直于直线
垂直于直线![]() ,垂足为
,垂足为![]() .设
.设![]() 点移动的时间为
点移动的时间为![]() 秒(
秒(![]() ),
),![]() 与直角梯形
与直角梯形![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
1.求经过 三点的抛物线解析式;
三点的抛物线解析式;
2.将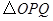 绕着点
绕着点 顺时针旋转
顺时针旋转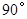 ,是否存在
,是否存在 ,使得
,使得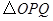 的顶点
的顶点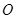 或
或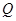 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
3.求 与
与 的函数关系式.
的函数关系式.
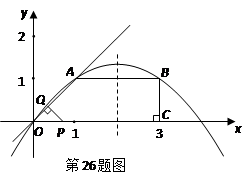
查看习题详情和答案>>
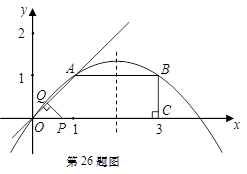
 中,
中,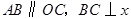 轴于点
轴于点 .动点
.动点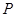 从
从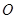 点出发,沿
点出发,沿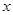 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过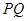 垂直于直线
垂直于直线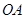 ,垂足为
,垂足为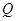 .设
.设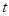 秒(
秒(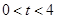 ),
),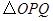 与直角梯形
与直角梯形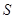 .
.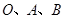 三点的抛物线解析式;
三点的抛物线解析式;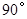 ,是否存在
,是否存在