摘要:方法与技巧: (1)观察图象.获取有用信息,(2)对获得信息加以整合.弄清各量之间的关系,(3)选择适当的数学工具,通过建模解决问题. [实弹射击]
网址:http://m.1010jiajiao.com/timu3_id_491285[举报]
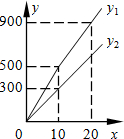 24、为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分 的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.
24、为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分 的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.(1)观察图象可知:a=
6
; b=8
; m=10
;(2)直接写出y1,y2与x之间的函数关系式;
(3)某旅行社导游王娜于5月1日带A团,5月20日(非节假日)带B团都到该景区旅游,共付门票款1900元,A,B两个团队合计50人,求A,B两个团队各有多少人?
 探索研究:
探索研究:通过对一次函数、反比例函数的学习.我们积累了一定的经验.下面我们借鉴以往研究函效的经验,探索的数y=x+
| 1 |
| x |
(1)填写下表,画出函数的图象:
| x | … |
|
|
|
1 | 2 | 3 | 4 | … | ||||||
| y | … | … |
①
函数两条不同类型的性质是:当0<x<1时,y 随x的增大而减小,当x>1时,y 随x的增大而增大;
函数两条不同类型的性质是:当0<x<1时,y 随x的增大而减小,当x>1时,y 随x的增大而增大;
;②
当x=1时,函数y=x+
(x>0)的最小值是2.
| 1 |
| x |
当x=1时,函数y=x+
(x>0)的最小值是2.
.| 1 |
| x |
知识运用:
一般函数y=x+
| a |
| x |
己知一个矩形的面积是4.设矩形的一边长为x.它的周长为y.求y与x的函数关系式,井求出:当x取何值时.矩形的周长最小?最小值是多少?
37、某同学将父母给的零用钱按每月相等的数额存放在储蓄盒内,准备捐给希望工程,盒内原来有40元,2个月后盒内有80元.
(1)求盒内钱数y(元)与存钱月数x之间的函数关系式(不要求写出x的取值范围).
(2)在直角坐标系中作出该函数的图象.
(3)观察图象回答:按上述方法,该同学经过
查看习题详情和答案>>
(1)求盒内钱数y(元)与存钱月数x之间的函数关系式(不要求写出x的取值范围).
y=40+20x
(2)在直角坐标系中作出该函数的图象.
(3)观察图象回答:按上述方法,该同学经过
8
个月能够存够200元.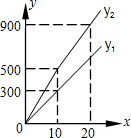 为发展旅游经济,“黄石国家矿山公园”对门票采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1,y2与x之间的函数图象如图所示.
为发展旅游经济,“黄石国家矿山公园”对门票采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1,y2与x之间的函数图象如图所示.(1)观察图象可知:a=
6
6
;b=8
8
;m=10
10
;(2)直接写出y1,y2与x之间的函数关系式;
(3)某旅行社导游于5月1日带A团,5月20日(非节假日)带B团都到该景区旅游,共付门票款1900元,A,B两个团队合计50人,求A,B两个团队各有多少人?
萧山所前的”杜家杨梅节”越办越红火了.某果品批发公司为指导2007年的杨梅销售,对历年的市场销售情况进行了调查统计,得到如下数据:
(1)观察表格中的数据,求出y与x的函数关系式;
(2)若杨梅平均进价为13元/千克,试求出销售利润P(元)与销售价x(元/千克)之间的函数关系式,并求出当销售价定为多少时,销售利润最大?
(3)请通过画该函数的草图的方法,观察图象的变化趋势,求出当销售价在什么范围内时,销售利润不少于24000元? 查看习题详情和答案>>
| 销售价x(元/千克) | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 |
| 销售量y(千克) | 2000 | 2500 | 3000 | 3500 | 4000 | 4500 | 5000 | 5500 |
(2)若杨梅平均进价为13元/千克,试求出销售利润P(元)与销售价x(元/千克)之间的函数关系式,并求出当销售价定为多少时,销售利润最大?
(3)请通过画该函数的草图的方法,观察图象的变化趋势,求出当销售价在什么范围内时,销售利润不少于24000元? 查看习题详情和答案>>