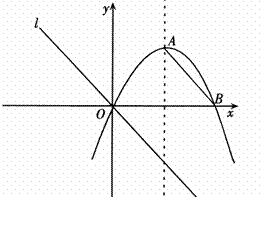
摘要：如图13.对称轴为的抛物线与轴相交于点.. (1)求抛物线的解析式.并求出顶点的坐标, (2)连结AB.把AB所在的直线平移.使它经过原点O.得到直线l.点P是l上一动点.设以点A.B.O.P为顶点的四边形面积为S.点P的横坐标为.当0＜S≤18时.求的取值范围, 的条件下.当取最大值时.抛物线上是否存在点.使△OP为直角三角形且OP为直角边.若存在,直接写出点的坐标,若不存在.说明理由.
网址：http://m.1010jiajiao.com/timu3_id_490382[举报]
如图13，对称轴为
的抛物线
与
轴相交于点
、
.
(1）求抛物线的解析式，并求出顶点
的坐标；
(2)连结AB，把AB所在的直线平移，使它经过原点O，得到直线
.点P是上一动点.设以点A、B、O、P为顶点的四边形面积为S，点P的横坐标为
，当0＜S≤18时，求的取值范围；
(3)在（2）的条件下，当取最大值时，抛物线上是否存在点
，使△
为直角三角形且OP为直角边.若存在,直接写出点的坐标；若不存在，说明理由.
 |
查看习题详情和答案>>
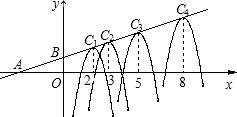如图，在平面直角坐标系xoy中，A（-3，0），B（0，1），形状相同的抛物线Cn（n=1，2，3，4，…）的顶点在直线AB上，其对称轴与x轴的交点的横坐标依次为2，3，5，8，13，…，根据上述规律，抛物线C2的顶点坐标为
如图，在直角坐标系中，O为原点，抛物线y=x2+bx+3与x轴的负半轴交于点A，与y轴的正半轴交于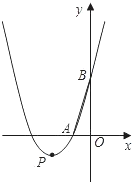
点B，tan∠ABO=
，顶点为P．
（1）求抛物线的解析式；
（2）若抛物线向上或向下平移|k|个单位长度后经过点C（-5，6），试求k的值及平移后抛物线的最小值；
（3）设平移后的抛物线与y轴相交于D，顶点为Q，点M是平移的抛物线上的一个动点．请探究：当点M在何位置时，△MBD的面积是△MPQ面积的2倍求出此时点M的坐标．友情提示：抛物线y=ax2+bx+c（a≠0）的对称轴是x=-
，顶点坐标是(-
，
)．
查看习题详情和答案>>
点B，tan∠ABO=| 1 |
| 3 |
（1）求抛物线的解析式；
（2）若抛物线向上或向下平移|k|个单位长度后经过点C（-5，6），试求k的值及平移后抛物线的最小值；
（3）设平移后的抛物线与y轴相交于D，顶点为Q，点M是平移的抛物线上的一个动点．请探究：当点M在何位置时，△MBD的面积是△MPQ面积的2倍求出此时点M的坐标．友情提示：抛物线y=ax2+bx+c（a≠0）的对称轴是x=-
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
如图，在平面直角坐标系中，A（-3，0），B（0，1），形状相同的抛物线Cn（n=1，2，3，4，…）的顶点在直线AB上，其对称轴与x轴的交点的横坐标依次为2，3，5，8，13，…，根据上述规律，抛物线C8的顶点坐标为（