摘要:26.如图.Rt△AB ¢C ¢ 是由Rt△ABC绕点A顺时针旋转得到的.连结CC ¢ 交斜边于点E.CC ¢ 的延长线交BB ¢ 于点F. (1)证明:△ACE∽△FBE,(2)设∠ABC=.∠CAC ¢ =.试探索.满足什么关系时.△ACE与△FBE是全等三角形.并说明理由.
网址:http://m.1010jiajiao.com/timu3_id_490030[举报]
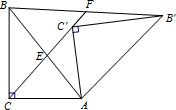 16、如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边AB于点E,CC′的延长线交BB′于点F.则下列推论:
16、如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边AB于点E,CC′的延长线交BB′于点F.则下列推论:①∠CBA=∠C′B′A;②∠CAC′=∠BAB′;③∠ACC′=∠ABB′.
正确的是
①②③
.(填序号)
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F.
(1)若AC=3,AB=4,求
;
(2)证明:△ACE∽△FBE;
(3)设∠ABC=α,∠CAC′=β,试探索α、β满足什么关系时,△ACE与△FBE是全等三角形,并说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)若AC=3,AB=4,求
| CC′ | BB′ |
(2)证明:△ACE∽△FBE;
(3)设∠ABC=α,∠CAC′=β,试探索α、β满足什么关系时,△ACE与△FBE是全等三角形,并说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
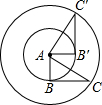 如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=1,BC=2,则旋转过程中
如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=1,BC=2,则旋转过程中
 如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F.证明:
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F.证明: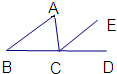 16、如图,若AB∥CE,需要的条件是( )
16、如图,若AB∥CE,需要的条件是( )