摘要：△ABC中.BC=a,AC=b,AB=c.若∠C=90°.如图1.根据勾股定理.则a2+b2=c2.若△ABC不是直角三角形.如图2和图3.请你类比勾股定理.试猜想a2+b2与c2的关系.并证明你的结论. 答案:b2-x2=AD2=c2-(a+x)2 b2-x2= c2-a2+2ax+x2 又∵2ax>0 ∴a2+b2>c2 b2-x2=AD2=C2-(a+x)2 b2-x2= c2-a2-2ax+x2 a2+b2= c2-2ax 又∵2ax>0 ∴a2+b2<c2
网址：http://m.1010jiajiao.com/timu3_id_488711[举报]
27、如图，在△ABC中DE∥BC，若DE=2，BC=3，则S三角形ADE：S四边形DBEC
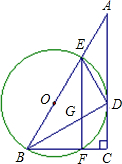在Rt△ABC中，BC=9，CA=12，∠ABC的平分线BD交AC与点D，DE⊥DB交AB于点E．（Ⅰ）设⊙O是△BDE的外接圆，求证：AC是⊙O的切线；
（Ⅱ）求⊙O的半径；
（Ⅲ）设⊙O交BC于点F，连接EF，求
| EF | AC |
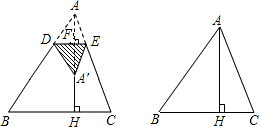点A关于DE的对称点A′落在AH所在的直线上）．
如图所示，已知在三角形纸片ABC中，BC=3，AB=6，∠BCA=90°，在AC上取一点E，以BE为折痕翻折△ABC，使AB的一部分与BC重合，A与BC延长线上的点D重合，则线段AD的长度为（ ）