摘要:(2010年三亚市月考)如图.在正方形ABCD中.E是AB边上任意一点.BG⊥CE.垂足为点O,交AC于点F.交AD于点G. (1) 证明:BE=AG , (2) 点E位于什么位置时.∠AEF=∠CEB.说明理由. 解(1)证明:∵四边形ABCD是正方形 ∴∠ABC=∠BAD=90°.∴∠1+∠3=90°. ∵BG⊥CE,∴∠BOC=90°∴∠2+∠3=90°, ∴∠1=∠2 ---------2分 在△GAB和△EBC中. ∵∠GAB=∠EBC=90°,AB=BC,∠1=∠2 ∴△GAB≌△EBC (ASA) ----4分 ∴AG=BE ---------- 5分 (2)解:当点E位于线段AB中点时.∠AEF=∠CEB -- 6分 理由如下:若当点E位于线段AB中点时.则AE=BE, 由(1)可知.AG=BE ∴AG=AE -------- 7分 ∵四边形ABCD是正方形.∴∠GAF=∠EAF=45°- 8分 又∵AF=AF,∴△GAF≌△EAF (SAS) ∴∠AGF=∠AEF ---------------10分 由(1)知.△GAB≌△EBC ∴∠AGF=∠CEB, ∴∠AEF=∠CEB ------------- 11分
网址:http://m.1010jiajiao.com/timu3_id_488676[举报]
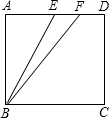 如图,在正方形ABCD中,E为AD的中点,F为ED的中点.
如图,在正方形ABCD中,E为AD的中点,F为ED的中点.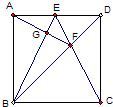 24、如图,在正方形ABCD中,E是AD边的中点,BD与CE交于F点.试判断AF与BE有何位置关系,并说明你的理由.
24、如图,在正方形ABCD中,E是AD边的中点,BD与CE交于F点.试判断AF与BE有何位置关系,并说明你的理由. 如图,在正方形ABCD中,F是CD的中点,E是BC边上的一点,且AF平分∠DAE
如图,在正方形ABCD中,F是CD的中点,E是BC边上的一点,且AF平分∠DAE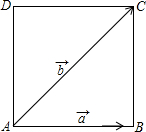 如图,在正方形ABCD中,AB=2,记
如图,在正方形ABCD中,AB=2,记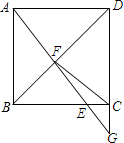 如图,在正方形ABCD中,点E是边BC上一点(与点B、C不重合),连接AE交对角线BD于点F,AE的延长线与DC的延长线相交于点G,连接FC.求证:
如图,在正方形ABCD中,点E是边BC上一点(与点B、C不重合),连接AE交对角线BD于点F,AE的延长线与DC的延长线相交于点G,连接FC.求证: