摘要:(2010年河南中考模拟题4)如图10.在中.点分别是边的中点.若把绕着点顺时针旋转得到. (1)请找出图中哪些线段与线段相等, (2)试判断四边形是怎样的四边形?并证明你的结论. 答案:(1)CF=BD=AD, (2)答:四边形是平行四边形 证明:∵绕着点顺时针旋转得到 ∴点D.E.F在一条直线上.且DF=2DE ∵点分别是边的中点 ∴DE是⊿ABC的中位线 ∴BC=2DE.且BC∥DE ∴DF∥BC ∴四边形是平行四边形
网址:http://m.1010jiajiao.com/timu3_id_488235[举报]
类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在 中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若
中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若 ,求
,求 的值。
的值。

(1)尝试探究
在图1中,过点E作 交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是
,
交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是
,  的值是
的值是
(2)类比延伸
如图2,在原题的条件下,若 则
则 的值是
(用含
的值是
(用含 的代数式表示),试写出解答过程。
的代数式表示),试写出解答过程。

(3)拓展迁移
如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若 ,则
,则 的值是
(用含
的值是
(用含 的代数式表示).
的代数式表示).

查看习题详情和答案>>
如图8,在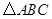 中,点
中,点 是
是 边的中点,点
边的中点,点 在
在 边上(不与端点重合).
边上(不与端点重合). 
【小题1】若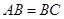 ,且
,且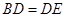 ,求证:
,求证: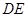 是
是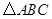 的中位线;
的中位线;
【小题2】若 ,则结论“
,则结论“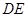 一定是
一定是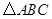 的中位线”是否正确?若正确请证明;若不正确,请举出反例.
的中位线”是否正确?若正确请证明;若不正确,请举出反例.

 中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若
中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若 ,求
,求 的值。
的值。
 交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 ,
交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 , 则
则 的代数式表示),试写出解答过程。
的代数式表示),试写出解答过程。
 ,则
,则 的值是 (用含
的值是 (用含 的代数式表示).
的代数式表示).
 中,点
中,点 是
是 边的中点,点
边的中点,点 在
在 边上(不与端点重合).
边上(不与端点重合). 
 ,且
,且 ,求证:
,求证: 是
是 ,则结论“
,则结论“