摘要:如图,在等腰梯形ABCD中,已知∠B=44°,上底AD长为4,梯形的高为2,求梯形底边BC的长. 解:过A.D两点分别作AE⊥BC,DF⊥BC,垂足为E.F. ∵梯形ABCD,∴AD∥BC, 又∵AE⊥BC,DF⊥BC, ∴AE∥DF,∴四边形AEFD是矩形. ∴AD=EF,AE=DF=2. 又∵等腰梯形ABCD,∴AB=CD,∠B=∠C, ∴△ABE≌△DCF,∴BE=CF. ∵在Rt△ABE中,cotB=, ∴BE=AEcotB=2cot44°, ∴BC=2BE+AD=4cot44°+4≈8.1. 答:梯形底边BC的长为8.1.
网址:http://m.1010jiajiao.com/timu3_id_488227[举报]
如图,在等腰梯形ABCD中,AD=6cm,BD=9cm,AB=8cm,E、F、G、H分别是AD、BD、BC、AC的中点,那么四边形EFGH的周长是 ( ).
(A)14cm (B)15cm (C)16cm (D)17cm
查看习题详情和答案>>
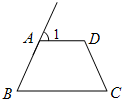 4、如图在等腰梯形ABCD中,AD∥BC,∠C=60°,则∠1=( )
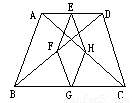
4、如图在等腰梯形ABCD中,AD∥BC,∠C=60°,则∠1=( ) ,对角线
,对角线 于点O,
于点O, ,垂足分别为E、F,设AD=a,BC=b,则四边形AEFD的周长是( )
,垂足分别为E、F,设AD=a,BC=b,则四边形AEFD的周长是( )
 B.
B. C.
C. D.
D.