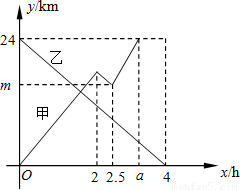
摘要:甲船从A港出发顺流匀速驶向B港.行至某处.发现船上一救生圈不知何时落入水中.立刻原路返回.找到救生圈后.继续顺流驶向B港.乙船从B港出发逆流匀速驶向A港.已知救生圈漂流的速度和水流速度相同,甲.乙两船在静水中的速度相同.甲.乙两船到A港的距离y1.y2之间的函数图象如图所示. (1)写出乙船在逆流中行驶的速度. (2)求甲船在逆流中行驶的路程. (3)求甲船到A港的距离y1与行驶时间x之间的函数关系式. (4)求救生圈落入水中时.甲船到A港的距离. [参考公式:船顺流航行的速度船在静水中航行的速度+水流速度.船逆流航行的速度船在静水中航行的速度水流速度.] 答案:(1)乙船在逆流中行驶的速度为6km/h. (2)甲船在逆流中行驶的路程为(km). (3)方法一: 设甲船顺流的速度为km/h. 由图象得. 解得a9. 当0≤x≤2时.. 当2≤x≤2.5时.设. 把.代入.得. ∴. 当2.5≤x≤3.5时.设. 把.代入.得. ∴. 方法二: 设甲船顺流的速度为km/h. 由图象得. 解得a9. 当0≤x≤2时.. 令.则. 当2≤x≤2.5时.. 即. 令.则. 当2.5≤x≤3.5时.. . (4)水流速度为. 设甲船从A港航行x小时救生圈掉落水中. 根据题意.得. 解得. . 即救生圈落水时甲船到A港的距离为13.5 km.
网址:http://m.1010jiajiao.com/timu3_id_488075[举报]
 26、甲船从A港出发顺流匀速驶向B港,行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后,继续顺流驶向B港.乙船从B港出发逆流匀速驶向A港.已知救生圈漂流的速度和水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.
26、甲船从A港出发顺流匀速驶向B港,行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后,继续顺流驶向B港.乙船从B港出发逆流匀速驶向A港.已知救生圈漂流的速度和水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.(1)写出乙船在逆流中行驶的速度;
(2)求甲船在逆流中行驶的路程;
(3)求甲船到A港的距离y1与行驶时间x之间的函数关系式;
(4)求救生圈落入水中时,甲船到A港的距离.
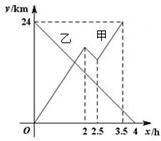
(2012•海陵区二模)甲船从A港出发顺流匀速驶向B港,乙船同时从B港出发逆流匀速驶向A港.甲船行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后,继续顺流驶向B港.已知甲、乙两船在静水中的速度相同,救生圈落入水中漂流的速度和水流速度都等于1.5km/h.甲、乙两船离A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.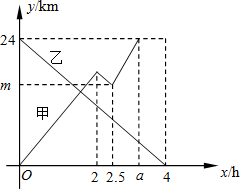
(1)甲船在顺流中行驶的速度为
(2)①当0≤x≤4时,求y2与x之间的函数关系式;②甲船到达B港时,乙船离A港的距离为多少?
(3)救生圈在水中共漂流了多长时间?
查看习题详情和答案>>

(1)甲船在顺流中行驶的速度为
9
9
km/h,m=15
15
;(2)①当0≤x≤4时,求y2与x之间的函数关系式;②甲船到达B港时,乙船离A港的距离为多少?
(3)救生圈在水中共漂流了多长时间?
 27、甲船从A港出发顺流匀速驶向B港,行至某处,发现船上-救生圈不知何时落入水中,立刻原路返回,找到救生圈后,继续顺流驶向B港.乙船从B港出发逆流匀速驶向A港.已知救生圈漂流的速度和水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.
27、甲船从A港出发顺流匀速驶向B港,行至某处,发现船上-救生圈不知何时落入水中,立刻原路返回,找到救生圈后,继续顺流驶向B港.乙船从B港出发逆流匀速驶向A港.已知救生圈漂流的速度和水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.(1)写出乙船在逆流中行驶的速度.
(2)求甲船在逆流中行驶的路程.
(3)求甲船到A港的距离y1与行驶时间x之间的函数关系式.
(4)求救生圈落入水中时,甲船到A港的距离.
参考公式:船顺流航行的速度=船在静水中航行的速度+水流速度,船逆流航行的速度=船在静水中航行的速度-水流速度.