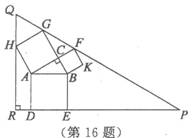
摘要：16．勾股定理有着悠久的历史.它曾引起很多人的兴趣．l955年希腊发行了二枚以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形构成.它可以验证勾股定理．在右图的勾股图中.已知∠ACB=90°.∠BAC=30°.AB= 4．作△PQR使得∠R=90°.点H在边QR上.点D.E在边PR上.点G.F在边 PQ上.那么APQR的周长等于 ▲ ． (摘录2010年浙江省温州市初中毕业生学业考试)
网址：http://m.1010jiajiao.com/timu3_id_487735[举报]
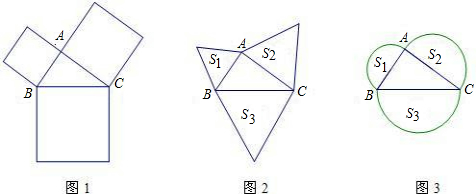
勾股定理有着悠久的历史，它曾引起很多人的兴趣．1955年希腊发行了二枚以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形构成（图1：△ABC中，∠BAC=90°）．
请解答：
（1）如图2，若以直角三角形的三边为边向外作等边三角形，则它们的面积S1、S2、S3之间的数量关系是 ．
（2）如图3，若以直角三角形的三边为直径向外作半圆，则它们的面积S1、S2、S3之间的数量关系是 ，请说明理由．
（3）如图4，在梯形ABCD中，AD∥BC，∠ABC+∠BCD=90°，BC=2AD，分别以AB、CD、AD为边向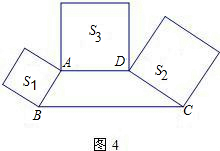
梯形外作正方形，其面积分别为S1、S2、S3，则S1、S2、S3之间的数量关系式为 ，请说明理由．
查看习题详情和答案>>
请解答：
（1）如图2，若以直角三角形的三边为边向外作等边三角形，则它们的面积S1、S2、S3之间的数量关系是
（2）如图3，若以直角三角形的三边为直径向外作半圆，则它们的面积S1、S2、S3之间的数量关系是
（3）如图4，在梯形ABCD中，AD∥BC，∠ABC+∠BCD=90°，BC=2AD，分别以AB、CD、AD为边向
梯形外作正方形，其面积分别为S1、S2、S3，则S1、S2、S3之间的数量关系式为
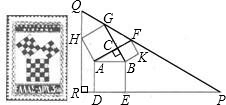
勾股定理有着悠久的历史，它曾引起很多人的兴趣．1955年希腊发行了二枚以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形构成，它可以验证勾股定理．在右图的勾股图中，已知∠ACB=90°，∠BAC=30°，AB=4．作△PQR使得∠R=90°，点H在边QR上，点D，E在边PR上，点G，F在边PQ上，那么△PQR的周长等于 ．
查看习题详情和答案>>
查看习题详情和答案>>
勾股定理有着悠久的历史，它曾引起很多人的兴趣．l955年希腊发行了二枚以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形构成，它可以验证勾股定理．在上图的勾股图中，已知∠ACB=90°，∠BAC=30°，AB=8．作△PQR使得∠R=90°，点H在边QR上，点D，E在边PR上，点G，F在边PQ上，那么△PQR的周长等于54+26
| 3 |
54+26
．| 3 |
勾股定理有着悠久的历史，它曾引起很多人的兴趣，如图所示，AB为Rt△ABC的斜边，四边形ABGM，APQC，BCDE均为正方形，四边形RFHN是长方形，若BC=3，AC=4，则图中空白部分的面积是
