摘要：已知正方形ABCD中.M是AB的中点.E是AB延长线上一点.MN⊥DM且交∠CBE的平分线于N. (1)求证:MD＝MN, (2)若将上述条件中的“M是AB的中点 改为“M是AB上任意一点 .其余条件不变.则结论“MD＝MN 还成立吗?如果成立.请证明,如果不成立.请说明理由.
网址：http://m.1010jiajiao.com/timu3_id_487110[举报]
已知正方形ABCD中，M是AB的中点，E是AB延长线上一点，MN⊥DM且交∠CBE的平分线于N，如图．
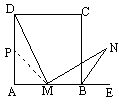
(1)求证：MD＝MN；
(2)若将上述条件中的“M是AB的中点”改为“M是AB上任意一点”，其余条件不变，如下图，则结论“MD＝MN”还成立吗？如果成立，请证明；如果不成立，请说明理由．
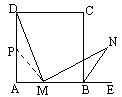
已知正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A旋转．
（1）发现与证明：
发现：①当E点旋转到DA的延长线上时（如图1），△ABE与△ADG的面积关系是： ．
②当E点旋转到CB的延长线上时（如图2），△ABE与△ADG的面积关系是： ．
证明：请你选择上述两个发现中的任意一个加以证明，选择①、②证明的满分分别为4分和6分．（注意：证明前要注明选择了哪一个发现）
（2）引申与运用：
引申：当正方形AEFG旋转任意一个角度时（如图3），△ABE与△ADG的面积关系是： ．
运用：已知△ABC，AB=5cm，BC=3cm，分别以AB、BC、CA为边向外作正方形（如图4），则图中阴影部分的面积和的最大值是 cm2．
证明：我选择 进行证明．
查看习题详情和答案>>
（1）发现与证明：
发现：①当E点旋转到DA的延长线上时（如图1），△ABE与△ADG的面积关系是：
②当E点旋转到CB的延长线上时（如图2），△ABE与△ADG的面积关系是：
证明：请你选择上述两个发现中的任意一个加以证明，选择①、②证明的满分分别为4分和6分．（注意：证明前要注明选择了哪一个发现）
（2）引申与运用：
引申：当正方形AEFG旋转任意一个角度时（如图3），△ABE与△ADG的面积关系是：
运用：已知△ABC，AB=5cm，BC=3cm，分别以AB、BC、CA为边向外作正方形（如图4），则图中阴影部分的面积和的最大值是
证明：我选择
查看习题详情和答案>>
已知正方形ABCD的对角线AC、BD交于O，点O是正方形EFGO的一个顶点，若正方形ABCD的边长为2．
（1）当OE∥AD、OG∥AB时，如图1，求图中两个正方形重叠部分的面积．
（2）若正方形EFGO饶点O逆时针转动时，如图2，两个正方形重叠部分的面积是否发生变化？试说明理由．
查看习题详情和答案>>
（1）当OE∥AD、OG∥AB时，如图1，求图中两个正方形重叠部分的面积．
（2）若正方形EFGO饶点O逆时针转动时，如图2，两个正方形重叠部分的面积是否发生变化？试说明理由．
查看习题详情和答案>>
于F、E，⊙O′的半径为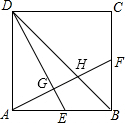
已知正方形ABCD的边长为2，E、F分别是AB，BC的中点，AF分别交DE，DB于G，H两点，则四边形BEGH的面积是（ ）