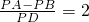摘要：如图.在⊙O中.两弦AB与CD的中点分别是P.Q.且.连结PQ.求证:∠APQ＝∠CQP.
网址：http://m.1010jiajiao.com/timu3_id_487008[举报]
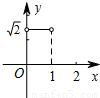
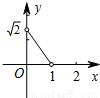
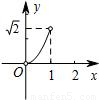
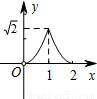
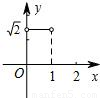
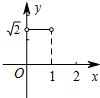如图，在半径为1的⊙O中，直径AB把⊙O分成上、下两个半圆，点C是上半圆上一个动点（C与点A、B不重合），过点C作弦CD⊥AB，垂足为E，∠OCD的平分线交⊙O于点P，设CE=x，AP=y，下列图象中，最能刻画y与x的函数关系的图象是（ ）A、 | B、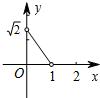 | C、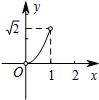 | D、 |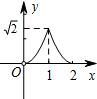
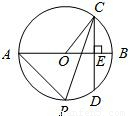
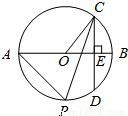
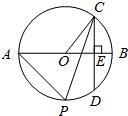
如图，在平面直角坐标系中，☉O的半径为5．弦AB平行于x轴，且AB=8．
（1）求B点坐标
（2）☉O交y轴负半轴于点C，P为
上一动点，连PA、PB、PC，过C作CD⊥BP，交BP的延长线于点D．求证：
=2
（3）过点B作弦BM、BN，与x轴分别交于E、F，BE=BF，连接MN与x轴交于H．当M、N两点运动时，判断①∠BOE+∠BNH是定值；②∠BOE+∠OHM是定值，哪一个结论正确，说明理由并求出定值．
查看习题详情和答案>>
（1）求B点坐标
（2）☉O交y轴负半轴于点C，P为
 |
| BC |
| PA-PB |
| PD |
（3）过点B作弦BM、BN，与x轴分别交于E、F，BE=BF，连接MN与x轴交于H．当M、N两点运动时，判断①∠BOE+∠BNH是定值；②∠BOE+∠OHM是定值，哪一个结论正确，说明理由并求出定值．
上一动点，连PA、PB、PC，过C作CD⊥BP，交BP的延长线于点D．求证：
