摘要：将抛物线绕顶点旋转1800.再沿对称轴平移.得到一条与直线交于点(2.)的新抛物线.新抛物线的解析式为 .
网址：http://m.1010jiajiao.com/timu3_id_486844[举报]
如图1，抛物线
：
与直线AB：
交于x轴上的一点A，和另一点B(3，n)．
(1)求抛物线的解析式；
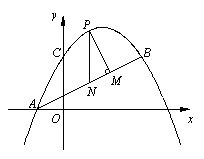
(2)点P是抛物线上的一个动点（点P在A，B两点之间，但不包括A，B两点），PM⊥AB于点M，PN∥y轴交AB于点N，在点P的运动过程中，存在某一位置，使得△PMN的周长最大，求此时P点的坐标，并求△PMN周长的最大值；
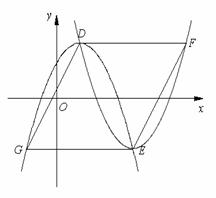
(3)如图2，将抛物线绕顶点旋转180°后，再作适当平移得到抛物线
，已知抛物线的顶点E在第四象限的抛物线上，且抛物线与抛物线交于点D，过D点作
轴的平行线交抛物线于点F，过E点作轴的平行线交抛物线于点G，是否存在这样的抛物线，使得四边形DFEG为菱形？若存在，请求E点的横坐标；若不存在请说明理由．
、
查看习题详情和答案>>(2007，吉林，23)如图，抛物线
向右平移1个单位得到抛物线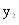
．回答下列问题：
(1)抛物线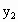
的顶点坐标________．
(2)阴影部分的面积S=________．
(3)若再将抛物线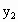绕原点O旋转180°得到抛物线
，则抛物线的开口方向________，顶点坐标________．
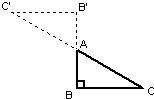如图，△ABC中，∠B=90，∠C=30°，AB=1，将△ABC绕顶点A旋转180°，点C落在C′处，则CC′的长为