摘要：方程组有两组不同的实数解.则( ) A.≥ B.＞ C.＜＜ D.以上答案都不对

网址：http://m.1010jiajiao.com/timu3_id_486757[举报]

阅读下列材料：
在平面直角坐标系中，若点P₁（x₁，y₁）、P₂（x₂，y₂），则P₁、P₂两点间的距离为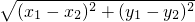 $数学公式$ ．例如：若
P₁（3，4）、P₂（0，0），则P₁、P₂两点间的距离为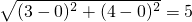 $数学公式$ ．
设⊙O是以原点O为圆心，以1为半径的圆，如果点P（x，y）在⊙O上，那么有等式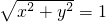 $数学公式$ ，即x²+y²=1成立；反过来，如果点P（x，y）的坐标满足等式x²+y²=1，那么点P必在⊙O上，这时，我们就把等式x²+y²=1称为⊙O的方程．
在平面直角坐标系中，若点P₀（x₀，y₀），则P₀到直线y=kx+b的距离为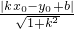 $数学公式$ ．
请解答下列问题：
（I）写出以原点O为圆心，以r（r＞0）为半径的圆的方程．
（II）求出原点O到直线 $数学公式$ 的距离．
（III）已知关于x、y的方程组： $数学公式$ ，其中n≠0，m＞0．
①若n取任意值时，方程组都有两组不相同的实数解，求m的取值范围．
②当m=2时，记两组不相同的实数解分别为（x₁，y₁）、（x₂，y₂），
求证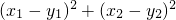： $数学公式$ 是与n无关的常数，并求出这个常数．

查看习题详情和答案>>

七年级学生参加了社会实践调查活动，到生态果园调查后得到如下信息：今年收获了15吨李子和8吨桃子，要租用甲、乙两种货车共6辆，及时运往外地，经询问，甲种货车可装李子4吨和桃子1吨，乙种货车可装李子1吨和桃子3吨．根据同学们带回的信息，试探究以下问题：
（1）共有几种租车方案？
（2）经咨询运输公司，甲种货车每辆需付运费1000元，乙种货车每辆需付运费700元，试帮助选出最佳方案，并求出此方案运费是多少．
请同学们补充完成下列部分解题过程：
（1）
①若设租用甲车x辆，则租用乙车______辆，
②由题意可知：甲车一共可装______吨桃子，乙车一共可装______吨桃子，则甲，乙两种车一共可装______吨桃子．（用含有x的代数式表示）
请列出不等式______
③甲车一共可装______吨李子，乙车一共可装______吨李子，则甲，乙两种车一共可装______吨李子．（用含有x的代数式表示）
请列出不等式______
④请列出不等式组，并求出满足不等组的整数解，写出相应的方案
（2）

查看习题详情和答案>>

七年级学生参加了社会实践调查活动，到生态果园调查后得到如下信息：今年收获了15吨李子和8吨桃子，要租用甲、乙两种货车共6辆，及时运往外地，经询问，甲种货车可装李子4吨和桃子1吨，乙种货车可装李子1吨和桃子3吨．根据同学们带回的信息，试探究以下问题：
（1）共有几种租车方案？
（2）经咨询运输公司，甲种货车每辆需付运费1000元，乙种货车每辆需付运费700元，试帮助选出最佳方案，并求出此方案运费是多少．
请同学们补充完成下列部分解题过程：
（1）解：
①若设租用甲车x辆，则租用乙车

辆，
②由题意可知：甲车一共可装

吨桃子，乙车一共可装

吨桃子，则甲，乙两种车一共可装

吨桃子．（用含有x的代数式表示）
请列出不等式

x+3（6-x）≥8

x+3（6-x）≥8

③甲车一共可装

吨李子，乙车一共可装

吨李子，则甲，乙两种车一共可装

吨李子．（用含有x的代数式表示）
请列出不等式

4x+（6-x）≥15

4x+（6-x）≥15

④请列出不等式组，并求出满足不等组的整数解，写出相应的方案
（2）解：

查看习题详情和答案>>

七年级学生参加了社会实践调查活动，到生态果园调查后得到如下信息：今年收获了15吨李子和8吨桃子，要租用甲、乙两种货车共6辆，及时运往外地，经询问，甲种货车可装李子4吨和桃子1吨，乙种货车可装李子1吨和桃子3吨．根据同学们带回的信息，试探究以下问题：
（1）共有几种租车方案？
（2）经咨询运输公司，甲种货车每辆需付运费1000元，乙种货车每辆需付运费700元，试帮助选出最佳方案，并求出此方案运费是多少．
请同学们补充完成下列部分解题过程：
（1）解：
①若设租用甲车x辆，则租用乙车辆，
②由题意可知：甲车一共可装吨桃子，乙车一共可装吨桃子，则甲，乙两种车一共可装吨桃子．（用含有x的代数式表示）
请列出不等式
③甲车一共可装吨李子，乙车一共可装吨李子，则甲，乙两种车一共可装吨李子．（用含有x的代数式表示）
请列出不等式__
④请列出不等式组，并求出满足不等组的整数解，写出相应的方案
（2）解：

查看习题详情和答案>>