摘要：例11. 如图.在平面直角坐标系中.A.B是x轴上的两点...以AO.BO为直径的半圆分别交AC.BC于E.F两点.若C点的坐标为求图像过A.B.C三点的二次函数的解析式.并求其对称轴,(2)求图像过点E.F的一次函数的解析式. 解:(1)由直角三角形的知识易得点A(.0).B(.0).由待定系数法可求得二次函数解析式为.对称轴是 (2)连结OE.OF.则..过E.F分别作x.y轴的垂线.垂足为M.N.P.G.易求得E(.).F(.)由待定系数法可求得一次函数解析式为
网址：http://m.1010jiajiao.com/timu3_id_486588[举报]
如图，在平面直角坐标系
中，
、
为
轴上两点，
、
为
一上两点，经过点、、的抛物线的一部分
与经过点、的抛物线的一部分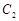
组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．已知点的坐标为
，点
是抛物线
的顶点．
（1）求、两点的坐标；
（2）“蛋线”在第四象限上是否存在一点
，使得
的面积最大？若存在，求出面积的最大值；若不存在，请说明理由；
（3）当
为直角三角形时，求
的值．
如图，在平面直角坐标系
中，
、
为
轴上两点，
、
为
一上两点，经过点、、的抛物线的一部分
与经过点、的抛物线的一部分
组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．已知点的坐标为
，点
是抛物线
的顶点．
（1）求、两点的坐标；
（2）“蛋线”在第四象限上是否存在一点
，使得
的面积最大？若存在，求出面积的最大值；若不存在，请说明理由；
（3）当
为直角三角形时，求
的值．
查看习题详情和答案>>
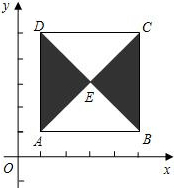如图，在平面直角坐标系中，正方形ABCD的对角线AC、BD交于点E，其中A（1，1）、B（5，1）、C（5，5）、D（1，5）．一个口袋中装有5个完全相同的小球，上面分别标有数字1、2、3、4、5，搅匀后从中摸出一个小球，把球上的数字做为点P的横坐标，放回后再摸出一个小球，将球上数字作为点P的纵坐标，则P点落在阴影部分（含边界）的概率是
如图，在平面直角坐标系中，四边形OABC是矩形，OA=4，AB=2，直线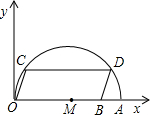
如图，在平面直角坐标系中，点A的坐标是（10，0），点B的坐标为（8，0），点C、D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，求点C的坐标．