摘要：说明:根据已知条件和选项中图象的特点.把不合条件的答案逐一排除.最后得到应选答案.
网址：http://m.1010jiajiao.com/timu3_id_486538[举报]
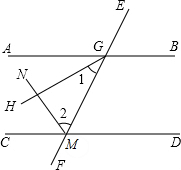说理填空：如图，已知AB∥CD，GH平分∠AGM，MN平分∠CMG，请说明GH⊥MN的理由．解：因为AB∥CD（已知），
所以∠AGF+
∠CHE
∠CHE
=180°（两直线平行，同旁内角互补
两直线平行，同旁内角互补
），因为GH平分∠AGF，MN平分∠CMG（
已知
已知
），所以∠1=
| 1 |
| 2 |
| 1 |
| 2 |
角平分线的定义
角平分线的定义
），得∠1+∠2=
| 1 |
| 2 |
90°
90°
，所以GH⊥MN（
垂直的定义
垂直的定义
）．根据已知条件和所得结论请总结出一个规律：
两直线平行，同旁内角的角平分线互相垂直
两直线平行，同旁内角的角平分线互相垂直
．如图，AB是OD的直径，点D在AB的延长线上且BD=OB，点C在圆上，∠CAB=30°．
(1)请根据已知条件和所给图形，猜想∠D的度数，再写出求解过程；
(2)DC是否是⊙O的切线?若是，请给出证明过程；若不是，请说明理由．
说理填空：如图，已知AB∥CD，GH平分∠AGM，MN平分∠CMG，请说明GH⊥MN的理由．
因为AB∥CD（已知），
所以∠AGF+______=180°（______ ），
因为GH平分∠AGF，MN平分∠CMG（______ ），
所以∠1=
∠AGF，∠2=
∠CMG（______），
得∠1+∠2=
（∠AGF+∠CMG）=______，
所以GH⊥MN（______）．
根据已知条件和所得结论请总结出一个规律：______．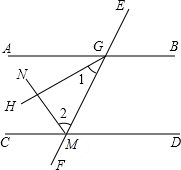
查看习题详情和答案>>
因为AB∥CD（已知），
所以∠AGF+______=180°（______ ），
因为GH平分∠AGF，MN平分∠CMG（______ ），
所以∠1=
| 1 |
| 2 |
| 1 |
| 2 |
得∠1+∠2=
| 1 |
| 2 |
所以GH⊥MN（______）．
根据已知条件和所得结论请总结出一个规律：______．
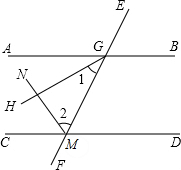说理填空：如图，已知AB∥CD，GH平分∠AGM，MN平分∠CMG，请说明GH⊥MN的理由．
∠AGF，∠2=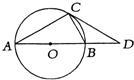
20、如图AB是⊙O的直径，AB=OD，BC=BD，请根据已知条件和所给图形，写出三个正确的结论：（不添加辅助线）①