摘要：4．如图2-5-11所示.直线y=-x+ 4与x 轴.y轴分别交于点M.N． (1)求M.N两点的坐标, (2)如果点P在坐标轴上.以点P为圆心.为半径的圆与直线y=-x+ 4相切.求点P的坐标．
网址：http://m.1010jiajiao.com/timu3_id_486406[举报]
如图12－1－11所示，螺线管CD的导线绕法不明．当磁铁AB插入螺线管时，电路中有图示方向的感应电流产生．下列关于螺线管极性的判断正确的是（ ）
查看习题详情和答案>>
| A．C端一定是N极 |
| B．C端的极性一定与磁铁B端的极性相同 |
| C．C端一定是S极 |
| D．无法判断，因螺线管的绕法不明确 |
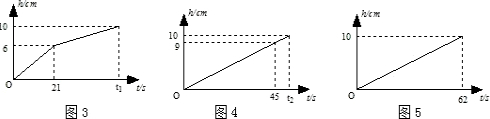
将一块a （cm）×b （cm ）×c （cm） （a＜b＜c）的长方体铁块（如图1所示）放入一长方体水槽（如图2所示）内，铁块与水槽四壁不接触、现向水槽内匀速注水，直至注满水槽为止．因为铁块在水槽内有三种不同的放置方式，所以，水槽内的水深h （cm）与注水时间t （s）的函数关系用图象法来反映其全过程有三个不同的图象（如图3，4，5所示）（三次注水速度相同）．
（1）根据图象填空：
（i）水槽的深度是 cm，a= ，b= ；
（ii） t1与t2的大小关系是t1 t2．
（2）求水槽内底面积、注水速度及c、t1、t2的值．
查看习题详情和答案>>
（1）根据图象填空：
（i）水槽的深度是
（ii） t1与t2的大小关系是t1
（2）求水槽内底面积、注水速度及c、t1、t2的值．
查看习题详情和答案>>
（2012•无锡）如图1，A、D分别在x轴和y轴上，CD∥x轴，BC∥y轴．点P从D点出发，以1cm/s的速度，沿五边形OABCD的边匀速运动一周．记顺次连接P、O、D三点所围成图形的面积为Scm2，点P运动的时间为ts．已知S与t之间的函数关系如图2中折线段OEFGHI所示．
（1）求A、B两点的坐标；
（2）若直线PD将五边形OABCD分成面积相等的两部分，求直线PD的函数关系式．
查看习题详情和答案>>
（1）求A、B两点的坐标；
（2）若直线PD将五边形OABCD分成面积相等的两部分，求直线PD的函数关系式．
将一块 a （cm）×b （cm ）×c （cm） （a＜b＜c）的长方体铁块（如图1所示）放入一长方体水槽（如图2所示）内，铁块与水槽四壁不接触．现向水槽内匀速注水，直至注满水槽为止．因为铁块在水槽内有三种不同的放置方式，所以水槽内的水深h （cm）与注水时间 t （s）的函数关系用图象法来反映其全过程有三个不同的图象，如图3、4、5所示（说明：三次注水速度相同）．
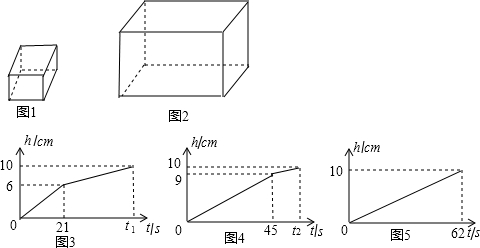
（1）根据图象填空
①水槽的深度是
②t1与t2的大小关系是t1
（2）求水槽内的底面积和注水速度；
（3）求c的值．
查看习题详情和答案>>
（1）根据图象填空
①水槽的深度是
10
10
cm，a=6cm
6cm
，b=9cm
9cm
；②t1与t2的大小关系是t1
=
=
t2，并求出t1、t2的值；（2）求水槽内的底面积和注水速度；
（3）求c的值．
有六名学生分成甲、乙两组（每组三个人），分乘两辆出租车同时从学校出发去世博园参观，出发10分钟后有一辆汽车出现故障，接着正常行驶的一辆车先把第一批学生送到世博园再回头接第二批学生，同时第二批学生步行前往．设出发后t分钟时汽车离开学校的路程为s千米，函数关系如图所示，第二批学生步行过程中离开学校的路程与出发时间t的图象如图中折线段AB-BC所示．（假设汽车载人和空载时的速度分别保持不变，学生步行速度不变，学生上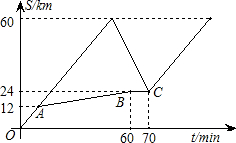
下车时间忽略不计．）
（1）从学校出发到全体到达世博园共花了 分钟；
（2）请解释图中线段BC的实际意义；
（3）为了节省时间，小明提出了一个想法：从故障点开始，在第二批学生步行的同时出租车先把第一批学生送到途中放下，让他们步行，再回头接第二批学生，使得两批学生同时到达博物馆．如果这样，学生在整个步行过程中不能休息，但步行的平均速度就会减少0.04km/min，请问按这种想法能提前多少分钟到达世博园？（假设汽车载人和空载时的速度分别保持不变．） 查看习题详情和答案>>
下车时间忽略不计．）（1）从学校出发到全体到达世博园共花了
（2）请解释图中线段BC的实际意义；
（3）为了节省时间，小明提出了一个想法：从故障点开始，在第二批学生步行的同时出租车先把第一批学生送到途中放下，让他们步行，再回头接第二批学生，使得两批学生同时到达博物馆．如果这样，学生在整个步行过程中不能休息，但步行的平均速度就会减少0.04km/min，请问按这种想法能提前多少分钟到达世博园？（假设汽车载人和空载时的速度分别保持不变．） 查看习题详情和答案>>