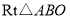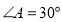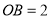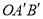摘要: 如图中...如果将在坐标平面内.绕原点按顺时针方向旋转到的位置. (1)求点的坐标. (2)求顶点从开始到点结束经过的路径长.
网址:http://m.1010jiajiao.com/timu3_id_485672[举报]
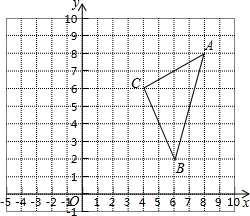 △ABC在坐标平面内的位置如图所示,请按要求完成下列任务:
△ABC在坐标平面内的位置如图所示,请按要求完成下列任务:
(1)画图:①以原点为位似中心,将△ABC作位似变换且缩小为原来的 ,得到△A′B′C′;
,得到△A′B′C′;
②以y轴为对称轴,将△A′B′C′作轴对称变换,得到△A″B″C″.
(2)填空:如果△ABC内一点M的坐标是(x,y),那么经过上述两次变换后其对应点M″的坐标为______.
查看习题详情和答案>>
平面直角坐标系内有两条直线l1、l2,直线l1的解析式为y=-
x+1,如果将坐标纸折叠,使直线l1与l2重合,此时点(-2,0)与点(0,2)也重合.
(1)求直线l2的解析式;
(2)设直线l1与l2相交于点M,问:是否存在这样的直线l:y=x+t,使得如果将坐标纸沿直线l折叠,点M恰好落在x轴上若存在,求出直线l的解析式;若不存在,请说明理由;
(3)设直线l2与x轴的交点为A,与y轴的交点为B,以点C(0,
)为圆心,CA的长为半径作圆,过点B任作一条直线(不与y轴重合),与⊙C相交于D、E两点(点D在点E的下方)
①在如图所示的直角坐标系中画出图形;
②设OD=x,△BOD的面积为S1,△BEC的面积为S2,
=y,求y与x之间的函数关系式 ,并写出自变量x的取值范围.
查看习题详情和答案>>
,并写出自变量x的取值范围.
查看习题详情和答案>>
| 2 |
| 3 |
(1)求直线l2的解析式;
(2)设直线l1与l2相交于点M,问:是否存在这样的直线l:y=x+t,使得如果将坐标纸沿直线l折叠,点M恰好落在x轴上若存在,求出直线l的解析式;若不存在,请说明理由;
(3)设直线l2与x轴的交点为A,与y轴的交点为B,以点C(0,
| 2 |
| 3 |
①在如图所示的直角坐标系中画出图形;
②设OD=x,△BOD的面积为S1,△BEC的面积为S2,
| S1 |
| S2 |
 ,并写出自变量x的取值范围.
查看习题详情和答案>>
,并写出自变量x的取值范围.
查看习题详情和答案>>
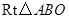 中,
中,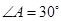 ,
,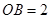 ,如果将
,如果将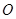 按顺时针方向旋转到
按顺时针方向旋转到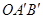 的位置.
的位置.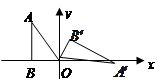
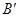 的坐标.
的坐标.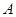 从开始到
从开始到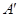 点结束经过的路径长.
点结束经过的路径长.