网址:http://m.1010jiajiao.com/timu3_id_485448[举报]
(16分)“5•12”汶川大地震后,某健身器材销售公司通过当地 “红十字会”向灾区献爱心,捐出了五月份全部销售利润.已知该公司五月份只售出甲、乙、丙三种型号器材若干台,每种型号器材不少于8台,五月份支出包括这批器材进货款64万元和其他各项支出(含人员工资和杂项开支)3.8万元.这三种器材的进价和售价如下表,人员工资y1(万元)和杂项支出y2(万元)分别与总销售量x(台)成一次函数关系(如图).
 (1)求y1与x的函数解析式;
(1)求y1与x的函数解析式;
(2)求五月份该公司的总销售量;
(3)设公司五月份售出甲种型号器材t台,五月份总销售利为W(万元),求W与t的函数关系式;(销售利润=销售额-进价-其他各项支出)
(4)请推测该公司这次向灾区捐款金额的最大值.
21世纪教育网
查看习题详情和答案>>
(16分)“5•12”汶川大地震后,某健身器材销售公司通过当地 “红十字会”向灾区献爱心,捐出了五月份全部销售利润.已知该公司五月份只售出甲、乙、丙三种型号器材若干台,每种型号器材不少于8台,五月份支出包括这批器材进货款64万元和其他各项支出(含人员工资和杂项开支)3.8万元.这三种器材的进价和售价如下表,人员工资y1(万元)和杂项支出y2(万元)分别与总销售量x(台)成一次函数关系(如图).
 (1)求y1与x的函数解析式;
(1)求y1与x的函数解析式;
(2)求五月份该公司的总销售量;
(3)设公司五月份售出甲种型号器材t台,五月份总销售利为W(万元),求W与t的函数关系式;(销售利润=销售额-进价-其他各项支出)
(4)请推测该公司这次向灾区捐款金额的最大值.
21世纪教育网
查看习题详情和答案>>
如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
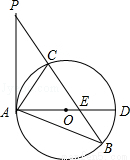
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG•AB=12,求AC的长;
(3)在满足(2)的条件下,若AF:FD=1:2,GF=1,求⊙O的半径及sin∠ACE的值.
查看习题详情和答案>>
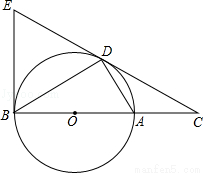
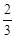 ,求BE的长.
,求BE的长.