摘要:如图.在中.是的中点.以为直径的交的三边.交点分别是点.的交点为.且.. (1)求证:. (2)求的直径的长. (3)若.以为坐标原点.所在的直线分别为轴和轴.建立平面直角坐标系.求直线的函数表达式. 25. (1)连接 是圆直径..即 ..················································································· 1分 .在中..··························· 2分 (2)是斜边的中点... 又由(1)知.. 又.与相似······················································ 3分 ············································································ 4分 又. ..······································ 5分 设... 直径.······························································································· 6分 (3)斜边上中线. 在中..······························ 7分 设直线的函数表达式为. 根据题意得. 解得 直线的函数解析式为································· 9分
网址:http://m.1010jiajiao.com/timu3_id_480145[举报]
 (2012•重庆)已知:如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=
(2012•重庆)已知:如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=| k |
| x |
| 2 |
| 5 |
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上有一点E(O点除外),使得△BCE与△BCO的面积相等,求出点E的坐标.
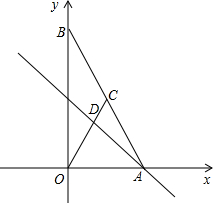 如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(0A<OB)是方程组
如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(0A<OB)是方程组
|
| 5 |
(1)求直线AB的解析式及点C的坐标;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以0、A、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
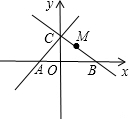 如图,在平面直角坐标系中直线AC交x轴于点A,交y轴于点C,过点C作直线CB⊥AC交x轴于点B,且AB=25,AO:CO=3:4,点P在线段OC上,且PO、PC的长是关于x的方程x2-12x+32=0的两根(PO<PC)
如图,在平面直角坐标系中直线AC交x轴于点A,交y轴于点C,过点C作直线CB⊥AC交x轴于点B,且AB=25,AO:CO=3:4,点P在线段OC上,且PO、PC的长是关于x的方程x2-12x+32=0的两根(PO<PC)(1)求AC、BC的长;
(2)若M为线段BC的中点,求直线PM的解析式;
(3)在平面内是否存在点Q,使以点A、C、P、Q为顶点的四边形是平行四边形?若存在请直接写出点Q的坐标;若不存在请说明理由. 查看习题详情和答案>>
如图,在等腰梯形ABCD中,AD∥BC,AB=DC=50,AD=75,BC=135.点P从点B出发沿折线段BA-AD-DC以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点Q向上作射线QKIBC,交折线段CD-DA-AB于点E.点P、Q同时开始运动,当点P与点C重合时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).
(1)当点P到达终点C时,求t的值,并指出此时BQ的长;
(2)当点P运动到AD上时,t为何值能使PQ∥DC?
(3)t为何值时,四点P、Q、C、E成为一个平行四边形的顶点?
(4)△PQE能为直角三角形时t的取值范围

查看习题详情和答案>>
(1)当点P到达终点C时,求t的值,并指出此时BQ的长;
(2)当点P运动到AD上时,t为何值能使PQ∥DC?
(3)t为何值时,四点P、Q、C、E成为一个平行四边形的顶点?
(4)△PQE能为直角三角形时t的取值范围
0<t≤25且t≠
或t=35
| 155 |
| 8 |
0<t≤25且t≠
或t=35
.(直接写出结果)(注:备用图不够用可以另外画)| 155 |
| 8 |

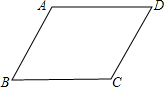 如图,在平行四边形ABCD中,如果∠A=125°,则∠D=( )
如图,在平行四边形ABCD中,如果∠A=125°,则∠D=( )