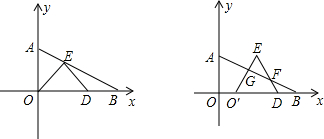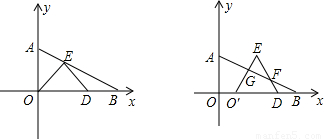摘要：(1).建立恰当的平面直角坐标系.并求出隧道拱抛物线的解析式, (2)在隧道拱的两侧距地面3米高处各安装一盏路灯.在(1)的平面直角坐标系中用坐标表示其中一盏路灯的位置, (3) 为了保证行车安全.要求行驶车辆顶部 与隧道拱在竖直方向上高度之差至少有0.5米．现有一辆汽车.装载货物后.其宽度为米.车载货物的顶部与路面的距离为2.5米.该车能否通过这个隧道?请说明理由．
网址：http://m.1010jiajiao.com/timu3_id_479935[举报]
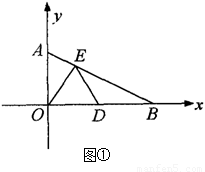
在Rt△ABO中，∠ABO=30°，BO=4，分别以OA、OB边所在的直线建立平面直角坐标系，D为x轴正半轴上一点，以OD为一边在第一象限内作等边△ODE.
（Ⅰ）如图①， 当E点恰好落在线段AB上，求点E的坐标；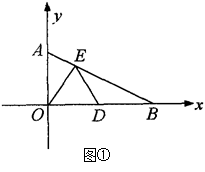
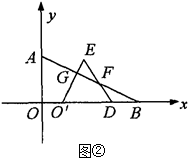
（Ⅱ）在（Ⅰ）问的条件下，将△ODE在线段OB上向右平移（如图②），图中是否存在一条与线段
始终相等的线段？如果存在，请指出这条线段，并加以证明；如果不存在，请说明理由.
（Ⅲ）若点D从原点出发沿x轴的正方向移动，设点D到原点的距离为x，△ODE与△AOB重叠部分面积为y，请直接写出y与x的函数关系式，并写出自变量x的取值范围.
在Rt△ABO中，∠ABO=30°，BO=4，分别以OA、OB边所在的直线建立平面直角坐标系，D为x轴正半轴上一点，以OD为一边在第一象限内作等边△ODE.
（Ⅰ）如图①， 当E点恰好落在线段AB上，求点E的坐标；
（Ⅱ）在（Ⅰ）问的条件下，将△ODE在线段OB上向右平移（如图②），图中是否存在一条与线段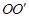
始终相等的线段？如果存在，请指出这条线段，并加以证明；如果不存在，请说明理由.
（Ⅲ）若点D从原点出发沿x轴的正方向移动，设点D到原点的距离为x，△ODE与△AOB重叠部分面积为y，请直接写出y与x的函数关系式，并写出自变量x的取值范围.
查看习题详情和答案>>
在Rt△ABO中，∠ABO=30°，BO=4，分别以OA、OB边所在的直线建立平面直角坐标系，D为x轴正半轴上一点，以OD为一边在第一象限内作等边△ODE.
（Ⅰ）如图①， 当E点恰好落在线段AB上，求点E的坐标；
（Ⅱ）在（Ⅰ）问的条件下，将△ODE在线段OB上向右平移（如图②），图中是否存在一条与线段
始终相等的线段？如果存在，请指出这条线段，并加以证明；如果不存在，请说明理由.
（Ⅲ）若点D从原点出发沿x轴的正方向移动，设点D到原点的距离为x，△ODE与△AOB重叠部分面积为y，请直接写出y与x的函数关系式，并写出自变量x的取值范围.
（Ⅰ）如图①， 当E点恰好落在线段AB上，求点E的坐标；
（Ⅱ）在（Ⅰ）问的条件下，将△ODE在线段OB上向右平移（如图②），图中是否存在一条与线段
始终相等的线段？如果存在，请指出这条线段，并加以证明；如果不存在，请说明理由.（Ⅲ）若点D从原点出发沿x轴的正方向移动，设点D到原点的距离为x，△ODE与△AOB重叠部分面积为y，请直接写出y与x的函数关系式，并写出自变量x的取值范围.
