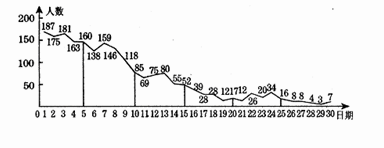
摘要：3．2006年春季.我市部分地区腮腺炎流行.党和政府采取果断措施.防治结合.很快使病情得到控制．下图是某同学记载的5月1日到30日每天我市腮腺炎新增确诊病例数据图．将图中记载的数据每5天作为一组.从左至右分为第一组至第六组.下列说法:①第一组的平均数最大.第六组的平均数最小,②第二组的中位数为138,③第四组的众数为28．其中正确的有( C ) A．0个 B．l个 C．2个 D．3个 例2如图.表示甲骑电动自行车和乙驾驶汽车均行驶90km的过程中.行使的路程与经过的时间之间的函数关系．请根据图象填空: 出发的早.早了 小时. 先到达.先到 小时.电动自行车的速度为 km / h.汽车的速度为 km / h． 知识点:本题考查是学生从图中获取信息的能力.及有条理的进行语言表述的能力． 精析:通过观察可以得出电动自行车与汽车都行驶了90(km).而电动自行车用了5个小时.汽车却用了一个小时.由此便可求出两车的速度． 解:甲.2.乙.2.18.90 ． 例3．改革开放以来.衢州的经济得到长足发展近来.衢州市委市政府又提出“争创全国百强城市"的奋斗目枥己下面是衢州市1999--2004年的生产总值与人均生产总值的统计资料: 请你根据上述统计资料回答下列问题: (1)1999-2004年间.衢州市人均生产总值增长速度最快的年份是 ．这一年的增长率为 ． (2)从1999年至2004年衢州市的总人口增加了约 万人(精确到O．01)．(3)除以上两个统计图中直接给出的数据以外.你还能从中获取哪些信息?请写出两条． 解:4．51(3)参考信息例举: ① ② ③ ④跨年度比较的增长度和增长率的数据, ⑤从增长趋势分析的数据． 点拨:此题属于图表信息题.读懂两图的区别与联系.是解决此题的关键． 例4在一次蜡烛燃烧实验中.甲.乙 两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)的关系如图2-1-2所示．请根据图象所提供的信息解答下列问题: ⑴甲.乙两根蜡烛燃烧前的高度分别是 .从点燃到燃尽所用的时间分别是 , ⑵分别求甲.乙两根蜡烛燃烧时y与x之间的函数关系式, ⑶当x为何值时.甲.乙两根蜡烛在燃烧过程中的高度相等? 解:⑴30cm.25cm,2h.2.5h, ⑵设甲蜡烛燃烧时y与x之间的函数关系式为. 由图可知.函数的图象过点. ∴ 解得 设乙蜡烛燃烧时y与x之间的函数关系式为. 由图可知.函数的图象过点. ∴解得 ⑶由题意得.解得 ∴ 当甲.乙两根蜡烛燃烧1h的时候高度相等． 点拨:要想求出一次函数解析式.关键是要找出图象上的两个关键点的坐标．这样我们就可以用待定系数法求出此函数的解析式了． 例5一次时装表演会预算中.票价定为每张 100元.容纳观众人数不超过2000人.毛利润y关于观众人数x之间的函数图象如图2-1-3所示.当观众人数超过1000人时.表演会组织者需向保险公司缴纳定额平安保险费5000元(不列人成本费用人请解答下列问题: (1)求当观众人数不超过1000人时.毛利润y关于观众人数的函数解析式和成本费用S关于观众人数x的函数解析式, (2)若要使这次表演会获得36000．元的毛利润.那么需售出多少张门票?需支付成本费用多少元? 注:当观众人数不超过1000人时.表演会的毛利润一门票收人一成本费用,当观众人数超过1000人时.表演会的毛利润＝门票收入-成本费用-平安保险费． 解:(1)由图2-1-3知.当 0≤x≤10与10＜x≤20时.y都是x的一次函数． 当0≤x≤10时.设y关于x的函数解析式为y＝kx+b.把点代入函数解析式.得 所以y＝50x-100(0≤x≤10). S＝100x-(50x-100)＝50x+100(0≤x≤10) (2)当10＜x≤20时.由题意.知 50x-100＝360． 所以x＝9．2.S＝50x+100 ＝50×9．2+100＝560． 当10＜x≤2 0时.设y＝mx+n． 把点代入函数解析式.得 所以y＝50x-150(10＜x≤20). S＝100x-(50x-150)-50＝50x+100(10＜x≤20) 当y＝360时.50x-150＝360.解得x＝10．2． 所以S＝50×10.2+100＝610． 答:需售门票 920张或 1020张.相应地需支付成本费用分别为56000元或 61000元． 点拨:正确理解题意.注意单位的统一． 练习

网址：http://m.1010jiajiao.com/timu3_id_479934[举报]