摘要：[解析]解决问题的关键是利用图中的相似三角形,解决问题中的m.n的关系求出点D的坐标.进而分别求出BD2.CE2.DE2的值,解决问题(4)时.通常方法是先猜想其结论成立.根据结论的特征.尝试构造直角三角形.则问题可轻松获解. [答案]解:(1)∆ABE∽∆DAE, ∆ABE∽∆DCA ∵∠BAE=∠BAD+45°,∠CDA=∠BAD+45° ∴∠BAE=∠CDA 又∠B=∠C=45° ∴∆ABE∽∆DCA (2)∵∆ABE∽∆DCA.∴ 由依题意可知CA=BA= ∴.∴m= 自变量n的取值范围为1<n<2. (3)由BD=CE可得BE=CD,即m=n ∵m=.∴m=n= ∵OB=OC=BC=1.∴OE=OD=-1.∴D(1-, 0) ∴BD=OB-OD=1-(-1)=2-=CE, DE=BC-2BD=2-2(2-)=2-2 ∵BD+CE=2 BD=2(2-)=12-8, DE=(2-2)= 12-8 ∴BD+CE=DE (4)成立 证明:如图,将∆ACE绕点A顺时针旋转90°至∆ABH的位置,则CE=HB,AE=AH, ∠ABH=∠C=45°,旋转角∠EAH=90°. 连接HD,在∆EAD和∆HAD中 ∵AE=AH, ∠HAD=∠EAH-∠FAG=45°=∠EAD, AD=AD. ∴∆EAD≌∆HAD ∴DH=DE 又∠HBD=∠ABH+∠ABD=90° ∴BD+HB=DH 即BD+CE=DE
网址：http://m.1010jiajiao.com/timu3_id_478906[举报]
旋转变换是世界运动变化的简捷形式之一，也是数学问题中一种重要的思想方法．解与图形的旋转相关的问题常用到全等三角形的知识，而利用旋转过程中的不变量、不变性是解决问题的关键．请你选择其中一题进行解答．
（1）如图1，已知P是等边三角形ABC内一点，PB=2，PC=1，∠BPC=150°，求PA的长；
（2）如图2，已知O是等边△ABC内的一点，∠AOB、∠BOC、∠AOC的角度之比为6：5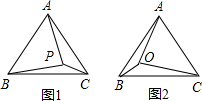
：4．求在以OA、OB、OC为边的三角形中，此三边所对的角度之比．
查看习题详情和答案>>
（1）如图1，已知P是等边三角形ABC内一点，PB=2，PC=1，∠BPC=150°，求PA的长；
（2）如图2，已知O是等边△ABC内的一点，∠AOB、∠BOC、∠AOC的角度之比为6：5
：4．求在以OA、OB、OC为边的三角形中，此三边所对的角度之比．
查看习题详情和答案>>
阅读理解，回答问题．
在解决数学问题的过程中，有时会遇到比较两数大小的问题，解决这类问题的关键是根据命题的题设和结论特征，采用相应办法，其中巧用“作差法”是解决此类问题的一种行之有效的方法：若a-b＞0，则a＞b；若a-b=0，则a=b；若a-b＜0，则a＜b．
例如：在比较m2+1与m2的大小时，小东同学的作法是：
∵（m2+1）-（m2）=m2+1-m2=1＞0，
∴m2+1＞m2．
请你参考小东同学的作法，解决如下问题：
（1）请你比较4
与（2+
）2的大小；
（2）已知a、b为实数，且ab=1，设M=
+
，N=
+
，试比较M、N的大小；
（3）一天，小明爸爸的男同事来家做客，已知爸爸的年龄比小明年龄的平方大7岁，爸爸同事的年龄是小明年龄的5倍，请你帮忙算一算，小明该称呼爸爸的这位同事为“叔叔”还是“大伯”？ 查看习题详情和答案>>
在解决数学问题的过程中，有时会遇到比较两数大小的问题，解决这类问题的关键是根据命题的题设和结论特征，采用相应办法，其中巧用“作差法”是解决此类问题的一种行之有效的方法：若a-b＞0，则a＞b；若a-b=0，则a=b；若a-b＜0，则a＜b．
例如：在比较m2+1与m2的大小时，小东同学的作法是：
∵（m2+1）-（m2）=m2+1-m2=1＞0，
∴m2+1＞m2．
请你参考小东同学的作法，解决如下问题：
（1）请你比较4
| 3 |
| 3 |
（2）已知a、b为实数，且ab=1，设M=
| a |
| a+1 |
| b |
| b+1 |
| 1 |
| a+1 |
| 1 |
| b+1 |
（3）一天，小明爸爸的男同事来家做客，已知爸爸的年龄比小明年龄的平方大7岁，爸爸同事的年龄是小明年龄的5倍，请你帮忙算一算，小明该称呼爸爸的这位同事为“叔叔”还是“大伯”？ 查看习题详情和答案>>
阅读理解，回答问题．
在解决数学问题的过程中，有时会遇到比较两数大小的问题，解决这类问题的关键是根据命题的题设和结论特征，采用相应办法，其中巧用“作差法”是解决此类问题的一种行之有效的方法：若a-b＞0，则a＞b；若a-b=0，则a=b；若a-b＜0，则a＜b．
例如：在比较m2+1与m2的大小时，小东同学的作法是：
∵（m2+1）-（m2）=m2+1-m2=1＞0，
∴m2+1＞m2．
请你参考小东同学的作法，解决如下问题：
（1）请你比较4
与（2+
）2的大小；
（2）已知a、b为实数，且ab=1，设M=
+
，N=
+
，试比较M、N的大小；
（3）一天，小明爸爸的男同事来家做客，已知爸爸的年龄比小明年龄的平方大7岁，爸爸同事的年龄是小明年龄的5倍，请你帮忙算一算，小明该称呼爸爸的这位同事为“叔叔”还是“大伯”？
查看习题详情和答案>>
在解决数学问题的过程中，有时会遇到比较两数大小的问题，解决这类问题的关键是根据命题的题设和结论特征，采用相应办法，其中巧用“作差法”是解决此类问题的一种行之有效的方法：若a-b＞0，则a＞b；若a-b=0，则a=b；若a-b＜0，则a＜b．
例如：在比较m2+1与m2的大小时，小东同学的作法是：
∵（m2+1）-（m2）=m2+1-m2=1＞0，
∴m2+1＞m2．
请你参考小东同学的作法，解决如下问题：
（1）请你比较4
与（2+）2的大小；（2）已知a、b为实数，且ab=1，设M=
+，N=+，试比较M、N的大小；（3）一天，小明爸爸的男同事来家做客，已知爸爸的年龄比小明年龄的平方大7岁，爸爸同事的年龄是小明年龄的5倍，请你帮忙算一算，小明该称呼爸爸的这位同事为“叔叔”还是“大伯”？
查看习题详情和答案>>
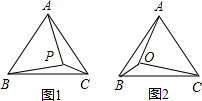：4．求在以OA、OB、OC为边的三角形中，此三边所对的角度之比．