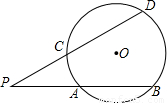
摘要:同学们知道:顶点在圆上.并且两边都和圆相交的角.叫圆周角.因为一条弧所对的圆周角等于它所对的圆心角的一半.而圆心角的度数等于它所对的弧的度数.所以圆周角的度数等于它所对的弧的度数的一半.类似的.我们定义:顶点在圆外.并且两边都和圆相交的角叫圆外角.如图6中.∠DPB是圆外角.那么∠DPB的度数与它所夹的两段弧BD和AC的度数有什么关系? (1)你的结论用文字表述为(不准出现字母和数学符号): . (2)证明你的结论.
网址:http://m.1010jiajiao.com/timu3_id_478064[举报]
我们知道:顶点在圆上,并且两边都和圆相交的角叫做圆周角,一条弧所对的圆周角的度数等于它所对的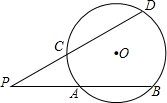 圆心角度数的一半.类似地,我们定义:顶点在圆外,并且两边都和圆相交的角叫做圆外角.
圆心角度数的一半.类似地,我们定义:顶点在圆外,并且两边都和圆相交的角叫做圆外角.
(1)判断:图中有没有圆外角如果有,请用字母表示出来.
(2)运用所学的数学知识,探究:圆外角的度数与它所夹的弧所对的圆心角的度数有什么关系将你的发现,用文字表述出来,并说明理由.(2007年唐洋镇中学初三模拟考试数学试卷改编) 查看习题详情和答案>>
 圆心角度数的一半.类似地,我们定义:顶点在圆外,并且两边都和圆相交的角叫做圆外角.
圆心角度数的一半.类似地,我们定义:顶点在圆外,并且两边都和圆相交的角叫做圆外角.(1)判断:图中有没有圆外角如果有,请用字母表示出来.
(2)运用所学的数学知识,探究:圆外角的度数与它所夹的弧所对的圆心角的度数有什么关系将你的发现,用文字表述出来,并说明理由.(2007年唐洋镇中学初三模拟考试数学试卷改编) 查看习题详情和答案>>
(2012•南京二模)情境一
我们知道:顶点在圆上,并且两边都和圆相交的角叫做圆周角.
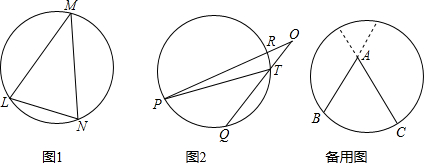
我们还知道:①圆心角的度数等于与它所对的弧的度数,②同弧所对的圆周角相等,都等于该弧所对的圆心角的一半.由此,小明得到一个正确的结论:圆周角的度数等于它所对的弧的度数的一半.如图1,∠LMN=
.
问题1 填空:如图1,如果
的度数是80,那么∠LMN的度数是
情境二
小明把顶点在圆外,并且两边都和圆相交的角叫圆外角,并继续探索.
如图2,∵∠PTQ是△OPT的一个外角,
∴∠PTQ=∠O+∠P.
∴∠O=∠PTQ-∠P.
∵圆周角的度数等于它所对的弧的度数的一半(已在情境一中证明),
∴∠PTQ=
,∠P=
.
∴∠O=∠PTQ-∠P=
-
=
(
-
).
经历了上述探索、证明过程,小明发现了“圆外角的度数等于它所夹的较大弧的度数减去较小弧的度数所得差的一半”这个正确结论.
问题2 填空:如图2,如果
=80°,
=20°,那么∠O=
问题3 类比情境二的内容,请你就角的顶点在圆内的情况进行探索.写出你的发现,并证明你的结论.
查看习题详情和答案>>
我们知道:顶点在圆上,并且两边都和圆相交的角叫做圆周角.
我们还知道:①圆心角的度数等于与它所对的弧的度数,②同弧所对的圆周角相等,都等于该弧所对的圆心角的一半.由此,小明得到一个正确的结论:圆周角的度数等于它所对的弧的度数的一半.如图1,∠LMN=
| 1 |
| 2 |
 |
| LN |
问题1 填空:如图1,如果
 |
| LN |
40
40
.情境二
小明把顶点在圆外,并且两边都和圆相交的角叫圆外角,并继续探索.
如图2,∵∠PTQ是△OPT的一个外角,
∴∠PTQ=∠O+∠P.
∴∠O=∠PTQ-∠P.
∵圆周角的度数等于它所对的弧的度数的一半(已在情境一中证明),
∴∠PTQ=
| 1 |
| 2 |
 |
| PQ |
| 1 |
| 2 |
 |
| RT |
∴∠O=∠PTQ-∠P=
| 1 |
| 2 |
 |
| PQ |
| 1 |
| 2 |
 |
| RT |
| 1 |
| 2 |
 |
| PQ |
 |
| RT |
经历了上述探索、证明过程,小明发现了“圆外角的度数等于它所夹的较大弧的度数减去较小弧的度数所得差的一半”这个正确结论.
问题2 填空:如图2,如果
 |
| PQ |
 |
| RT |
30
30
°.问题3 类比情境二的内容,请你就角的顶点在圆内的情况进行探索.写出你的发现,并证明你的结论.

类比学习:
我们已经知道,顶点在圆上,且角的两边都和圆相交的角叫做圆周角,如图1,∠APB就是圆周角,弧AB是∠APB所夹的弧.
类似的,我们可以把顶点在圆外,且角的两边都和圆相交的角叫做圆外角,如图2,∠APB就是圆外角,弧AB和弧CD是∠APB所夹的弧,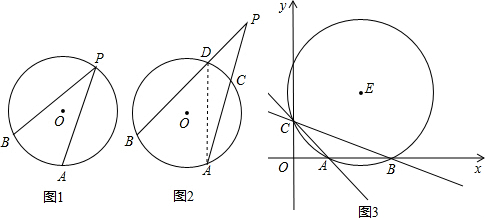
新知探索:
图(2)中,弧AB和弧CD度数分别为80°和30°,∠APB=
归纳总结:
(1)圆周角的度数等于它所夹的弧的度数的一半;
(2)圆外角的度数等于
新知应用:
直线y=-x+m与直线y=-
x+2相交于y轴上的点C,与x轴分别交于点A、B.经过A、B、C三点作⊙E,点P是第一象限内⊙E外的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC分别交⊙E于点M、N,
设∠APC=θ.
①求A点坐标; ②求⊙E的直径;
③连接MN,求线段MN的长度(可用含θ的三角函数式表示).
查看习题详情和答案>>
我们已经知道,顶点在圆上,且角的两边都和圆相交的角叫做圆周角,如图1,∠APB就是圆周角,弧AB是∠APB所夹的弧.
类似的,我们可以把顶点在圆外,且角的两边都和圆相交的角叫做圆外角,如图2,∠APB就是圆外角,弧AB和弧CD是∠APB所夹的弧,

新知探索:
图(2)中,弧AB和弧CD度数分别为80°和30°,∠APB=
25
25
°,归纳总结:
(1)圆周角的度数等于它所夹的弧的度数的一半;
(2)圆外角的度数等于
所夹两弧的度数差的一半
所夹两弧的度数差的一半
.新知应用:
直线y=-x+m与直线y=-
| ||
| 3 |
设∠APC=θ.
①求A点坐标; ②求⊙E的直径;
③连接MN,求线段MN的长度(可用含θ的三角函数式表示).
类比学习:
我们已经知道,顶点在圆上,且角的两边都和圆相交的角叫做圆周角,如图1,∠APB就是圆周角,弧AB是∠APB所夹的弧.
类似的,我们可以把顶点在圆外,且角的两边都和圆相交的角叫做圆外角,如图2,∠APB就是圆外角,弧AB和弧CD是∠APB所夹的弧,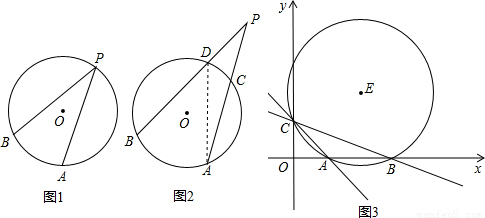
新知探索:
图(2)中,弧AB和弧CD度数分别为80°和30°,∠APB=______°,
归纳总结:
(1)圆周角的度数等于它所夹的弧的度数的一半;
(2)圆外角的度数等于______.
新知应用:
直线y=-x+m与直线y=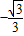 x+2相交于y轴上的点C,与x轴分别交于点A、B.经过A、B、C三点作⊙E,点P是第一象限内⊙E外的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC分别交⊙E于点M、N,
x+2相交于y轴上的点C,与x轴分别交于点A、B.经过A、B、C三点作⊙E,点P是第一象限内⊙E外的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC分别交⊙E于点M、N,
设∠APC=θ.
①求A点坐标; ②求⊙E的直径;
③连接MN,求线段MN的长度(可用含θ的三角函数式表示).
查看习题详情和答案>>
我们已经知道,顶点在圆上,且角的两边都和圆相交的角叫做圆周角,如图1,∠APB就是圆周角,弧AB是∠APB所夹的弧.
类似的,我们可以把顶点在圆外,且角的两边都和圆相交的角叫做圆外角,如图2,∠APB就是圆外角,弧AB和弧CD是∠APB所夹的弧,

新知探索:
图(2)中,弧AB和弧CD度数分别为80°和30°,∠APB=______°,
归纳总结:
(1)圆周角的度数等于它所夹的弧的度数的一半;
(2)圆外角的度数等于______.
新知应用:
直线y=-x+m与直线y=
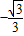 x+2相交于y轴上的点C,与x轴分别交于点A、B.经过A、B、C三点作⊙E,点P是第一象限内⊙E外的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC分别交⊙E于点M、N,
x+2相交于y轴上的点C,与x轴分别交于点A、B.经过A、B、C三点作⊙E,点P是第一象限内⊙E外的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC分别交⊙E于点M、N,设∠APC=θ.
①求A点坐标; ②求⊙E的直径;
③连接MN,求线段MN的长度(可用含θ的三角函数式表示).
查看习题详情和答案>>