摘要：22．如图.点P在经过点B的直线上.且纵坐标为-1.Q点在y=的图象上.若PQ∥y轴.求Q点的坐标．
网址：http://m.1010jiajiao.com/timu3_id_477657[举报]
如图，点A是反比例函数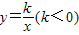
y上一点，作AB⊥x轴于点B，且△AOB的面积为2，点A坐标为（-1，m）．
（1）求k和m的值．
（2）若直线y=ax+3经过点A，交另一支双曲线于点C，求△AOC的面积．
（3）指出x取何值时，一次函数的值大于反比例函数的值，直接写出结果．
（4）在y轴上是否存在点P，使得△PAC的面积为6？如果存在，请求出点P的坐标；若不存在，请说明理由．
查看习题详情和答案>>
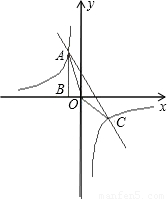
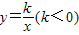y上一点，作AB⊥x轴于点B，且△AOB的面积为2，点A坐标为（-1，m）．（1）求k和m的值．
（2）若直线y=ax+3经过点A，交另一支双曲线于点C，求△AOC的面积．
（3）指出x取何值时，一次函数的值大于反比例函数的值，直接写出结果．
（4）在y轴上是否存在点P，使得△PAC的面积为6？如果存在，请求出点P的坐标；若不存在，请说明理由．
查看习题详情和答案>>
如图，点A是反比例函数
y上一点，作AB⊥x轴于点B，且△AOB的面积为2，点A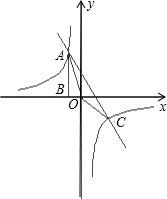
坐标为（-1，m）．
（1）求k和m的值．
（2）若直线y=ax+3经过点A，交另一支双曲线于点C，求△AOC的面积．
（3）指出x取何值时，一次函数的值大于反比例函数的值，直接写出结果．
（4）在y轴上是否存在点P，使得△PAC的面积为6？如果存在，请求出点P的坐标；若不存在，请说明理由．
查看习题详情和答案>>
如图，点C将线段AB分成两部分，如果
，那么称点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1，S2，如果
，那么称直线l为该图形的黄金分割线．
(1)研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点(如图2)，则直线CD是△ABC的黄金分割线．你认为对吗？为什么？
(2)请你说明：三角形的中线是否也是该三角形的黄金分割线？
(3)研究小组在进一步探究中发现：过点C任作一条直线交AB于点E，再过点D作直线DF∥CE，交AC于点F，连接EF(如图3)，则直线EF也是△ABC的黄金分割线．
请你说明理由．
(4)如图4，点E是□ABCD的边AB的黄金分割点，过点E作EF∥AD，交DC于点F，显然直线EF是□ABCD的黄金分割线．请你画一条□ABCD的黄金分割线，使它不经过□ABCD各边黄金分割点．
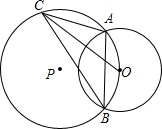如图，⊙P与⊙O相交于A、B两点，⊙P经过圆心O，点C是⊙P的优弧上
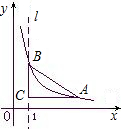如图，直线l是经过点（1，0）且与y轴平行的直线．Rt△ABC中直角边AC=4，BC=3．将BC边在直线l上滑动，使A，B在函数