摘要：如图.四边形ABCD是正方形.G是BC上任意一点.AE⊥DG于E.CF∥AE交DG于F. (1)在图中找出一对全等三角形.并加以证明, (2)求证:AE=FC+EF.
网址：http://m.1010jiajiao.com/timu3_id_476657[举报]
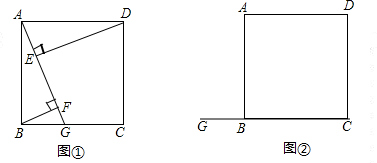
如图①，四边形ABCD是正方形，点G是BC上任意一点，DE⊥AG于点E，BF⊥AG于点F．
（1）求证：DE-BF=EF；
（2）当点G为BC边中点时，试探究线段EF与GF之间的数量关系，并说明理由；
（3）若点G为CB延长线上一点，其余条件不变．请你在图②中画出图形，写出此时DE、BF、EF之间的数量关系（不需要证明）．
查看习题详情和答案>>
（1）求证：DE-BF=EF；
（2）当点G为BC边中点时，试探究线段EF与GF之间的数量关系，并说明理由；
（3）若点G为CB延长线上一点，其余条件不变．请你在图②中画出图形，写出此时DE、BF、EF之间的数量关系（不需要证明）．
查看习题详情和答案>>
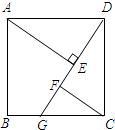21、如图，四边形ABCD是正方形，G是BC上任意一点（点G与B、C不重合），AE⊥DG于E，CF∥AE交DG于F．（1）在图中找出一对全等三角形，并加以证明；
（2）请你经过观察、猜测线段FC、AE、EF之间是否存在一定的数量关系？若存在，证明你的结论；若不存在，请说明理由．
15、如图，四边形ABCD是正方形，G是BC上任意一点（点G与B、C不重合），AE⊥DG于E，CF∥AE交DG于F．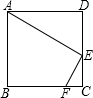
如图，四边形ABCD是正方形，点E、F分别在边DC、BC上，AE⊥EF，如果
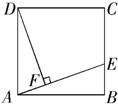21、如图，四边形ABCD是正方形，点E在BC上，DF⊥AE，垂足为F，请你在AE上确定一点G，使△ABG≌△DAF，请你写出两种确定点G的方案，并写出其中一种方案的具体作法和证明△ABG≌△DAF．