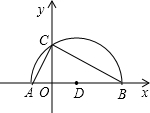
摘要:25:.已知如图.抛物线与y轴交于点c.与x轴交于点A.B. 点A的坐标为(2.0). (1) 求抛物线的解析式. (2) 点Q.是线段OB上的动点.过点Q作QE//BC.交AC于点E连接CQ.设 OQ=m.当三角形CQE的面积最大时.求m的值.并写出Q点的坐标. (3)若平行于x轴的动直线.与该抛物线交于点只与直线BC交于点F.A D的坐 标为..则是否存在这样的直线L.使OD=DF?若存在.求出点P的坐标, 若不存在.请说明理由. 26.如图直角梯形OABC和边长为4的正方形DEFG.G.0.A三点在一条直线 B上.OA//BC.ABOA.CB=2.OA=4.OC=.当D点与O点重合时.此正 方形开始向右沿直线b运动.当G点与A点重合时.运动停止.设OD:z.此正 方形DEFG和直角梯形OABC重合部分的面积为s.回答下列问题: (1) . (2)在正方形DEFG疏平行移动过程中.观察s的变化情况: 1逐渐增大,②逐渐减少,③先增大后减少,④先减少后增大. 正确的是: (3) 求S与x之间的函数关系式. (4) 直接写出J的最大值.
网址:http://m.1010jiajiao.com/timu3_id_474489[举报]
 BC=4
BC=4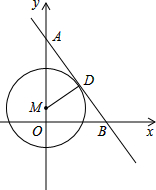 如图,已知直线y=-2x+12分别与Y轴,X轴交于A,B两点,点M在Y轴上,以点M为圆心的⊙M与直线AB相切于点D,连接MD.
如图,已知直线y=-2x+12分别与Y轴,X轴交于A,B两点,点M在Y轴上,以点M为圆心的⊙M与直线AB相切于点D,连接MD.