摘要：15．证明:如图1. ∵ AB=AC . ∴ ∠B=∠C ．- - - - - - - - - - - - - - - - - - - - - -1分 在△BDF和△CED中. ∴ △BDF≌△CED ． - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 3分 ∴ DF = ED．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 4分 ∴ ∠DEF=∠DFE．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 5分
网址：http://m.1010jiajiao.com/timu3_id_474042[举报]
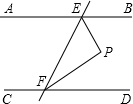求证：若两条直线平行，则一对同旁内角的角平分线互相垂直．（1）将下列语句补写完整．
已知：如图，直线
AB∥CD
AB∥CD
，直线EF分别交AB，CD于点E、F，PE平分∠BEF，PF平分∠EFD
PF平分∠EFD
求证：∠P=
90°
90°
（2）证明：
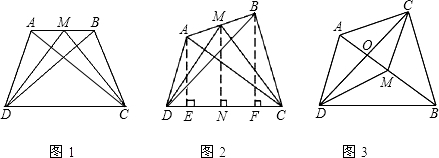
（2013•乐山模拟）如图甲，AB⊥BD，CD⊥BD，AP⊥PC，垂足分别为B、P、D，且三个垂足在同一直线上，我们把这样的图形叫“三垂图”．
（1）证明：AB•CD=PB•PD．
（2）如图乙，也是一个“三垂图”，上述结论成立吗？请说明理由．
（3）已知抛物线与x轴交于点A（-1，0），B（3，0），与y轴交于点（0，-3），顶点为P，如图丙所示，若Q是抛物线上异于A、B、P的点，使得∠QAP=90°，求Q点坐标．
查看习题详情和答案>>
（1）证明：AB•CD=PB•PD．
（2）如图乙，也是一个“三垂图”，上述结论成立吗？请说明理由．
（3）已知抛物线与x轴交于点A（-1，0），B（3，0），与y轴交于点（0，-3），顶点为P，如图丙所示，若Q是抛物线上异于A、B、P的点，使得∠QAP=90°，求Q点坐标．
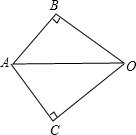如图，OB⊥AB，OC⊥AC，垂足为B，C，OB=OC，证明：AO平分∠BAC．
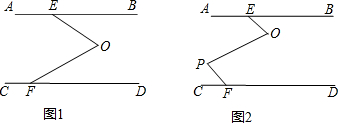如图1，AB∥CD，EOF是直线AB、CD间的一条折线．