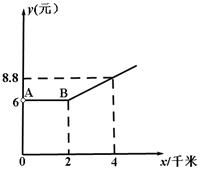
摘要：当 时,函数 有意义.
网址：http://m.1010jiajiao.com/timu3_id_473314[举报]
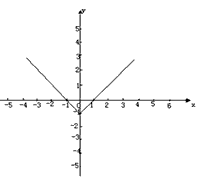
，当x=2时没有意义，则a的值为（ ）。你已经学会了作一次函数y=x-1的图象，知道它是一条直线，你能作出函数y=∣x∣-1的图象吗？根据绝对值的意义，当x≥0，∣x∣=x，则y=x-1；当x<0时，∣x∣=-x，则y= -x-1，因此我们可以在y轴的左侧作出y=-x-1的图象，在y轴的右侧作出y= x-1的图象，这两条直线结合起来即为函数y=∣x∣-1的图象，如图所示，
（1）这个图象有什么特点？
（2）你能通过对直线y=x-1进行适当的变化得到这个函数的图象吗？
（3）根据你在（1）（2）中得到的启发，请作出函数 y=-2∣x∣+1的图象。
（1）这个图象有什么特点？
（2）你能通过对直线y=x-1进行适当的变化得到这个函数的图象吗？
（3）根据你在（1）（2）中得到的启发，请作出函数 y=-2∣x∣+1的图象。
我市的出租车收费y(元)与路程x(千米)之间的函数关系如图所示。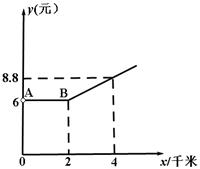
（1）图中AB段的意义是 。
（2）当x＞2时，y与x的函数关系式为 。
（3）蒋老师打算乘出租车从甲地去丙地，但需途经乙地办点事。已知甲地到乙地的路程为1km，乙地至丙地的路程超过3km。现有两种打车方案：
方案一：先打车从甲地到乙地，办完事后，再打另一部出租车去丙地；
方案二：先打车从甲地到乙地，让出租车司机等候，办完事后，继续乘该车去丙地（出租车等候期间，蒋老师每分钟支付0.2元）。
蒋老师应选择哪种方案较为合算？试说明理由。
